B.2 ITERATIVE/CONSTRUCTIVE SCHEDULING ALGORITHMS
An iterative/constructive algorithm generates a schedule by adding the nodes of the DFG to the schedule one node at a time until all nodes have been scheduled. They differ from one another by the methods employed to choose the nodes that will be scheduled and where they will be scheduled. Two of the more simple methods are “As Soon as Possible” and “As Late as Possible” scheduling. These scheduling algorithms are illustrated using the example of an iterative formulation of a 2nd-order differential equation solver.
Consider the 2nd-order differential equation and its corresponding C program formulation:
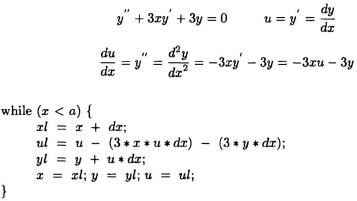
whose DFG is shown in Fig. B.2. In this DFG, the multiplication and addition operations are assumed to be executed in one time step. Many synthesis systems construct and use a more simplified version of the DFG by removing all edges with weights greater than zero. This leaves a DFG that only contains the precedence constraints for one iteration or the intra-iteration precedence constraints and is known as the precedence graph. Fig. B.2(b) shows the precedence graph for the DFG of Fig. B.2(a). Note that the precedence graph is always guaranteed to be acyclic.
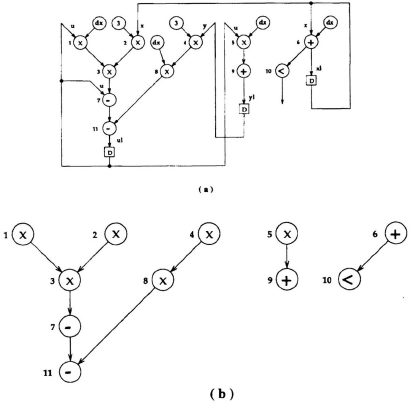
Fig. B 2 (a) The DFG of the 2nd-order differential equation formulation. (b) ...
Get VLSI Digital Signal Processing Systems: Design and Implementation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

