9.6 PROBLEMS
- Express the 2-parallel filter algorithm:
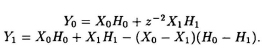
in terms of a postprocessing matrix, a diagonal matrix, and a preprocessing matrix. Obtain another 2-parallel structure using the transpose of this formulation.
- Consider a 6-tap FIR filter with unit-sample response
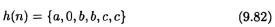
and
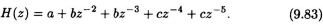
The sequential filter has 3 distinct coefficients and can be implemented using 3 multiplication operations as shown in Fig. 9.35. The 2-parallel filter will not require more than 6 multiplication operations. Design the structure of a 2-parallel implementation of this filter. Show the coefficients of all multipliers in your structure.
- Design a 3-parallel filter structure using the transpose of the 3-parallel filter algorithm presented in Section 9.2.2.1.
- Using the following 3-parallel linear convolution:
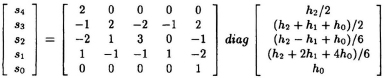
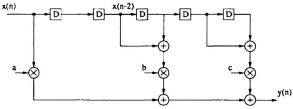
Fig. 9.35 Figure for Problem 2.
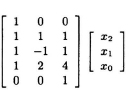
obtain a 3-parallel filter that requires 5 subfiltering operations.
- Use ...
Get VLSI Digital Signal Processing Systems: Design and Implementation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

