Statistical Inference: A Short Course

7.2 The Sampling Distribution of The Mean

Suppose μ is some unknown population mean. We want to determine its “true value.” How should we proceed to find μ? A reasonable approach is to take a simple random sample and make an inference from the sample to the population. How is this inference made? We use an estimator for μ. Think of an estimator as a function of the sample values used to estimate μ. A logical estimator for μ is the sample mean . (Specifying an estimator is a form of data reduction—we summarize the information about μ contained in a sample by determining some essential characteristic of the sample values. 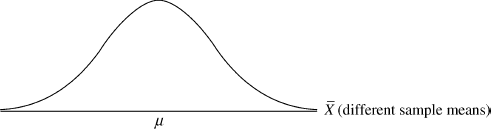So for purposes of inference about μ, we employ the realization of rather than the entire set of observed data points.) Under random sampling, is a random variable and thus has a probability distribution that we shall term the sampling distribution of the mean—a distribution showing the probabilities of obtaining different sample means from random samples of size n taken from a population of size N (Fig. 7.1).

Figure 7.1 Sampling distribution of the mean.

We shall call ...