The opening paragraph from the section WHAT’S WRONG WITH DUPLICATES? applies equally well here, with just one tiny text substitution, so I’ll basically just repeat it: There are numerous practical arguments in support of the position that nulls should be prohibited. Here I want to emphasize just one—but I think it’s a powerful one. But it does rely on certain notions I haven’t discussed yet in this book, so I need to make a couple of preliminary assumptions:
I assume you know that any comparison in which at least one of the comparands is null evaluates to the UNKNOWN truth value instead of TRUE or FALSE. The justification for this state of affairs is the intended interpretation of null as value unknown: If the value of A is unknown, then it’s also unknown whether, for example, A > B, regardless of the value of B (even—perhaps especially—if the value of B is unknown as well). Note: That same state of affairs is also the source of the term three-valued logic (3VL). That is, the notion of nulls, as understood in SQL, inevitably leads to a logic in which there are three truth values instead of the usual two. (The relational model, by contrast, is based on conventional two-valued logic, 2VL.)
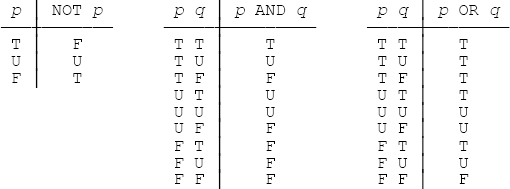
I assume you’re also familiar with the 3VL truth tables for the familiar logical operators—also known as connectives—NOT, AND, and OR (T = TRUE, F = FALSE, U = UNKNOWN):
Observe in particular that NOT returns UNKNOWN if its input is UNKNOWN; AND returns UNKNOWN if one input is UNKNOWN and the other is either UNKNOWN or TRUE; and OR returns UNKNOWN if one input is UNKNOWN and the other is either UNKNOWN or FALSE.
Now I can present my argument. The fundamental point I want to make is that certain boolean expressions—and therefore certain queries in particular—can produce results that are correct according to three-valued logic but not correct in the real world. By way of example, consider the (nonrelational) database shown in Figure 4-2, in which “the CITY is null” for part P1. Note carefully that the shading in that figure, in the place where the CITY value for part P1 ought to be, stands for nothing at all; conceptually, there’s nothing at all—not even a string of blanks or an empty string—in that position (which means the “tuple” for part P1 isn’t really a tuple, a point I’ll come back to near the end of this section).
Consider now the following (admittedly rather contrived) query on the database of Figure 4-2: “Get (SNO,PNO) pairs where either the supplier and part cities are different or the part city isn’t Paris (or both).” Here’s an SQL formulation of this query:
SELECT S.SNO , P.PNO
FROM S , P
WHERE S.CITY <> P.CITY
OR P.CITY <> 'Paris'Now I want to focus on the boolean expression in the WHERE clause:
( S.CITY <> P.CITY ) OR ( P.CITY <> 'Paris' )
(I’ve added some parentheses for clarity.) For the only data we have, this expression evaluates to UNKNOWN OR UNKNOWN, which reduces to just UNKNOWN. Now, queries in SQL retrieve data for which the expression in the WHERE clause evaluates to TRUE, not to FALSE and not to UNKNOWN;[55] in the example, therefore, nothing is retrieved at all.
But part P1 does have some corresponding city in the real world;[56] in other words, “the null CITY” for part P1 does stand for some real value, say c. Now, either c is Paris or it isn’t. If it is, then the expression
( S.CITY <> P.CITY ) OR ( P.CITY <> 'Paris' )
becomes (for the only data we have)
( 'London' <> 'Paris' ) OR ( 'Paris' <> 'Paris' )
which evaluates to TRUE, because the first term evaluates to TRUE. Alternatively, if c isn’t Paris, then the expression becomes (again, for the only data we have)
( 'London' <>c) OR (c<> 'Paris' )
which also evaluates to TRUE, because the second term evaluates to TRUE. Thus, the boolean expression is always true in the real world, and the query should therefore return the pair (S1,P1), regardless of what real value the null stands for. In other words, the result that’s correct according to the logic (meaning, specifically, 3VL) and the result that’s correct in the real world are different!
By way of another example, consider the following query on that same table P from Figure 4-2 (I didn’t lead with this example because it’s even more contrived than the previous one, but in some ways it makes the point with even more force):
SELECT PNO
FROM P
WHERE CITY = CITYThe real world answer here is surely the set of part numbers currently appearing in P (in other words, the set containing just part number P1, given the sample data shown in Figure 4-2). SQL, however, will return no part numbers at all.
To sum up: If you have any nulls in your database, then you’re getting wrong answers to certain of your queries. What’s more, you have no way of knowing, of course, just which queries you’re getting wrong answers to and which not; all results become suspect. You can never trust the answers you get from a database with nulls. In my opinion, this state of affairs is a complete showstopper.
Aside: To all of the above, I can’t resist adding that even though SQL does support 3VL, and even though it does support the keyword UNKNOWN, that keyword does not—unlike the keywords TRUE and FALSE—denote a value of type BOOLEAN. (This is just one of the numerous flaws in SQL’s 3VL support; there are many, many others, but most of them are beyond the scope of this book.) To elaborate briefly: As with 2VL, the SQL type BOOLEAN contains just two values, TRUE and FALSE; “the third truth value” is represented, quite incorrectly, by null! Here are some consequences of this fact:
Assigning UNKNOWN to a variable B of type BOOLEAN actually sets B to null.
After such an assignment, the comparison B = UNKNOWN doesn’t give TRUE—instead, it gives null (meaning, to spell the point out, that SQL apparently believes, or claims, that it’s unknown whether B is UNKNOWN). Note, incidentally, that this state of affairs constitutes a violation of The Assignment Principle (see Exercise 2.22 in Chapter 2, also Chapter 5).
In fact, the comparison B = UNKNOWN always gives null (meaning UNKNOWN), regardless of the value of B, because it’s logically equivalent to the comparison “B = NULL” (not meant to be valid SQL syntax).
To understand the seriousness of such flaws, you might care to meditate on the analogy of a numeric type that uses null instead of zero to represent zero. End of aside.
As with the business of duplicates earlier, there’s a lot more that could be said on the whole issue of nulls, but I just want to close with a brief look at the formal argument against them. Recall that, by definition, a null isn’t a value. It follows that:
A “type” that contains a null isn’t a type (because types contain values).
A “tuple” that contains a null isn’t a tuple (because tuples contain values).
A “relation” that contains a null isn’t a relation (because relations contain tuples, and tuples don’t contain nulls).
In fact, nulls (like duplicates) violate one of the most fundamental relational principles of all—viz., The Information Principle. Once again, see Appendix A for further discussion of that principle.
The net of all this is that if nulls are present, then we’re certainly not talking about the relational model (I don’t know what we are talking about, but it’s not the relational model); the entire edifice crumbles, and all bets are off.
[55] A more accurate statement is: If the boolean expression in a WHERE clause evaluates to UNKNOWN, that UNKNOWN gets coerced to FALSE. Incidentally, it’s interesting to note that, by contrast, if the boolean expression in a CHECK clause—see Chapter 8—evaluates to UNKNOWN, that UNKNOWN gets coerced not to FALSE but to TRUE! This state of affairs (this inconsistency, rather) might reasonably be regarded as yet another nail in the nulls coffin. See the answer to Exercise 8.21g in Appendix F for further discussion.
[56] I’m relying here on the fact that (as noted earlier) the intended interpretation of null is value unknown, from which it follows that the fact that “the CITY is null” for part P1 means part P1 does have some city, but we don’t know what it is. (In fact, if part P1 had no city at all—i.e., if the property of having a city didn’t apply to part P1—then that part shouldn’t have been mentioned in the table in the first place. See the discussion of relvar predicates in Chapter 5.)
Get SQL and Relational Theory, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.