8.2. POLE-PLACEMENT DESIGN USING LINEAR-STATE-VARIABLE FEEDBACK
Having presented methods for designing linear control systems using classical techniques, let us now look at the problem of specifying pole placement from the viewpoint of state-variable feedback [1]. In order to do this, let us first look at the basic feedback problem illustrated in Figure 8.1. This figure illustrates the concept of feeding back the states of the process in addition to that of the output. Because a linear process can be characterized by the phase-variable canonical equations
![]()
![]()
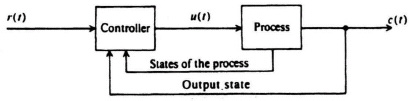
Figure 8.1 General feedback system problem illustrating feedback of the output state and the states of the process.
let us consider the configuration of Figure 8.2. It is important to observe from this figure that the control signal is generated from a knowledge of the reference input r(t) and the state variables x(t). Note that r(t), u(t), and c(t) represent scalars.
In general, the control input u can be represented as
u(t) = f (x(t), r(t)).
Rather than considering the controller in such a broad sense, let us consider the specific condition of linear state-variable feedback where the controller weights the sum of the state variables ...
Get Modern Control System Theory and Design, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

