6.4. MAPPING CONTOURS FROM THE s-PLANE TO THE F(s)-PLANE
Prior to introducing the Nyquist stability criterion which is very useful for determining the degree of stability or instability of feedback control systems, it is important to understand how to map contours from the s-plane to the F(s)-plane where F(s) is some rational function of s. A contour map is defined as a contour in the s-plane which is then mapped or transferred into the F(s)-plane by the definition of the rational function F(s). Because s is the complex variable s = σ + jω and F(s) is a complex function, then we can represent F(s) as F(s) = u + jv. Therfore, the F(s)-plane is also a complex plane having coordinates of u and v.
To illustrate the mapping process from the s-plane to the F(s)-plane, consider the unit-square contour in the s-plane illustrated in Figure 6.5a. We wish to map this unit-square contour from the s-plane to the F(s)-plane where F(s) is a rational function of s and is defined by the following expression:
![]()
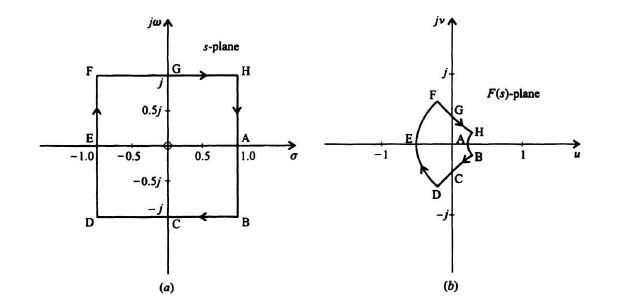
Figure 6.5 (a) Contour in the s-plane to be mapped for F(s) = s/(s + 3). (b) Resulting mapping in the F(s)-plane for F(s) = s/(s + 3) for the contour shown in the s-plane in Figure 6.5(a).
Since we are defining F(s) = u + jv, then
Table 6.1 provides several values of F(s) as s traverses the ...
Get Modern Control System Theory and Design, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

