5.5. TRANSIENT RESPONSE
In addition to stability, sensitivity, and accuracy, we are always concerned with the transient response of a feedback system. Transient response characteristics are defined on the basis of a step input. The response of a second-order system, containing one pure integration, to a unit step is useful for purposes of defining the various transient parameters. Should a problem arise where the system is higher than second order, a reasonably good approximation can be made by assuming that the system is second order if one pair of complex-conjugate roots dominates. This point is amplified during the discussion of the root locus in Chapters 6, 7 and 8. For purposes of illustration, let us consider the second-order system analyzed in Section 4.2. There we had a unity-feedback system whose closed loop transfer function C(s)/R(s) was given by [see Eq. (4.3)]
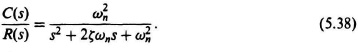
Its response to a unit step input, for the case of ζ < 1, was given by [see Eq. (4.24)]
![]()
where
![]()
The input and output responses are illustrated in Figure 5.7.
The time for the feedback system to reach its first peak of the overshoot is commonly referred to as the time to peak tp As was derived in Section 4.2 [see ...
Get Modern Control System Theory and Design, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

