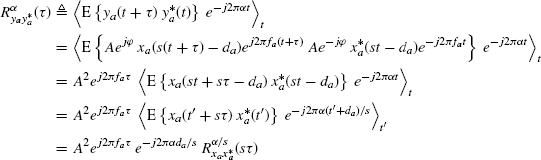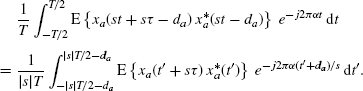7.10 Proofs
7.10.1 Proof of (7.262)
Fourier transform of a time-scaled, delayed, and frequency-shifted signal:
(7.383) ![]()
(7.384) ![]()
(7.385) 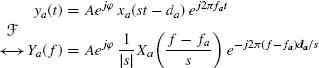
7.10.2 Proof of (7.263) and (7.264)
By using (7.261), the result is that
where ![]() is the continuous-time infinite average with respect to t, and, in the third equality, the variable change t′ = st − da is made, so that
is the continuous-time infinite average with respect to t, and, in the third equality, the variable change t′ = st − da is made, so that
This proof can be equivalently carried out in the FOT approach by simply removing the expectation operator E{ · } in (7.386) and (7.387).
(7.264) is obtained by Fourier transforming both sides of (7.263).
7.10.3 Proof of (7.262) and (7.272)
By reasoning as for (7.386), we have
(7.388) 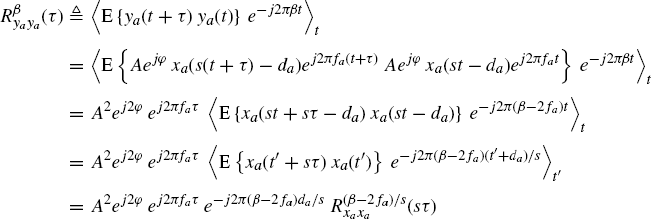
(7.268) is obtained by Fourier transforming both sides of (7.267).
7.10.4 Proof of (7.273)
Get Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.