4.12 Numerical Results
In this section, simulation results are reported to corroborate the theoretical results of the previous sections on the spectral cross-correlation density estimation.
4.12.1 Simulation Setup
The spectral cross-correlation density function between complex-envelope signals x(t) and y(t) is measured, where x(t) and y(t) are the input and output signals, respectively, of a linear time-variant system that models the channel between transmitter and receiver in relative motion with constant relative radial speed, that is (Section 7.3)
In (4.304), a is the (possibly complex) scaling amplitude, d the delay, s the time-scale factor, and ν the frequency shift.
For an ACS input process x(t) the Loève bifrequency cross-spectrum between y(t) and x(t) is given by (see (7.276))
(4.305) 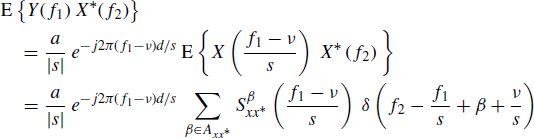
where ![]() and
and ![]() are the cyclic spectra and the set of cycle frequencies, respectively, of x(t). Therefore, if s ≠ 1, x(t) and y(t) are not jointly ACS (even if they are singularly ACS) but are jointly SC and exhibit joint spectral correlation on curves f2 = Ψ(n)(f1) which are lines with slope ...
are the cyclic spectra and the set of cycle frequencies, respectively, of x(t). Therefore, if s ≠ 1, x(t) and y(t) are not jointly ACS (even if they are singularly ACS) but are jointly SC and exhibit joint spectral correlation on curves f2 = Ψ(n)(f1) which are lines with slope ...
Get Generalizations of Cyclostationary Signal Processing: Spectral Analysis and Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

