8.1. Theoretical background
Unlike IIR filters, finite impulse response (FIR) filters are specific to the discrete-time domain and cannot be obtained by direct transposition of analog filters. The linear phase of the transfer function makes them useful for many applications.
8.1.1. Transfer function and properties of FIR filters
For this type of filter, also called non-recursive due to the implementation method, the transfer function is defined by:
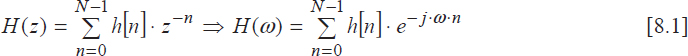
where h[n] stands for the (finite) impulse response of the filter.
In order to avoid the phase discontinuities of the transfer function, H(ω) is expressed in the following form:
![]()
where the zero-phase transfer function H0 (ω) and the phase function θ(ω) are real and continuous.
In practice, the impulse response h[n] is required to be real, which means that the real part of H (ω) is even, while its imaginary part is odd. The linearity constraint for the phase function θ(ω) leads to the four FIR filter classes, whose properties are summarized in Table 8.1.
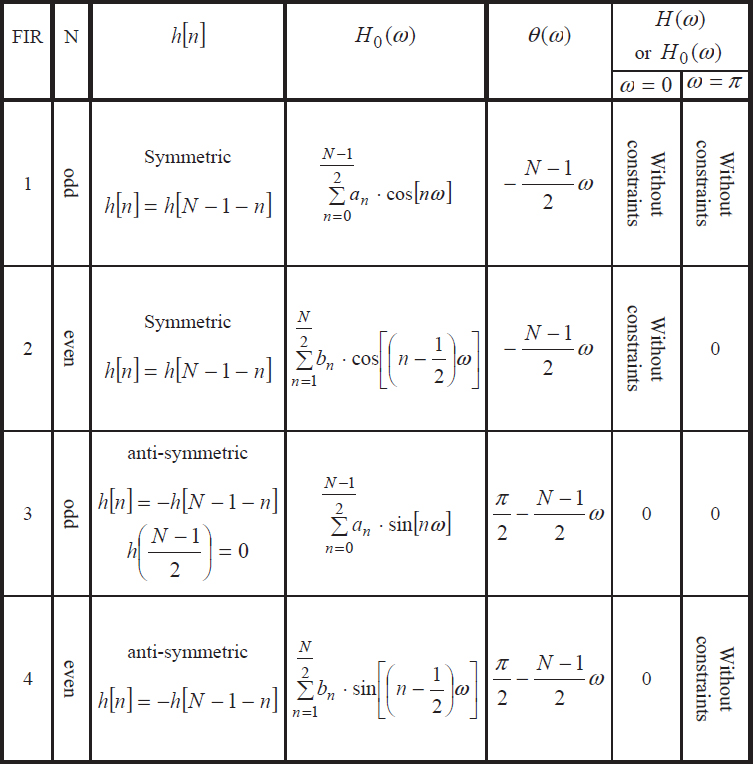
Table 8.1. Properties of FIR filters
Coefficients ai and bi in Table 8.1 can be obtained using the following equations:
The first two classes' filters are usually involved in pure filtering ...
Get Digital Signal Processing Using Matlab now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

