10.1. Introduction
A filter of impulse response h(k) is bounded-input, bounded-output (BIBO) stable when a bounded input signal x(k) produces a bounded output y(k).
Let us consider a bounded input signal x(k);

where h*(− k) and |h (−k)| respectively designate the conjugate and the complex modulus of h(−k). With equation (10.1), the output y(k) is written as:
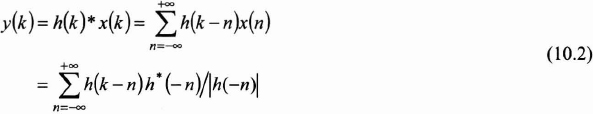
More specifically, equation (10.2) verifies for k = 0:

If the filter is BIBO stable, then it verifies the following condition:

Inversely, if the impulse response h(k) of the filter satisfies equation (10.4) then, for any input signal x(k) bounded by M, the output y(k) verifies:
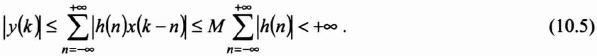
Let us assume now that the filter admits a transfer function1:

We write C the open convergence ring (i.e. circular band) represented as:
![]()
or it can be represented ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

