9.4. Appendix: spatial window functions and their implementation
The goal of this appendix is to explain the action in the frequency space of the apodization window. To illustrate the transformation resulting from weighting, we will consider, in a general way, a signal. Generally, apodization is represented by:
![]()
where Y0 (x, y) is the finite observation of a signal represented on an infinite 2-D horizon written as y (x,y). In the frequency domain, a convolution product regulates the transformation:
![]()
Because of the convolution operator, we observe a frequency distortion of the spectrum Y(u, v). The window which we choose by default is a rectangular window.
Figure 9.22. Spatial profile of a rectangular window
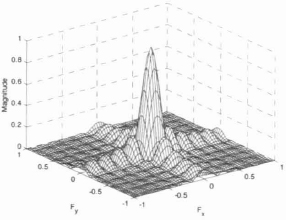
Figure 9.23. Associated 2-D frequency spectrum
As shown in Figure 9.23, in the frequency plane, the rectangular window is characterized by a fairly narrow principle lobe that is inversely proportional to the length of the window. Its second characteristic is the low differential between its amplitude maxima of its secondary lobes in relation to that of the principle lobe. As we saw ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

