Digital Filters Design for Signal and Image Processing

8.5. Filtering in the frequency domain

When the filter properties are specified in the frequency domain, or when the impulse responses have a very large support, it is advantageous to carry out the filtering operation in the Fourier domain by using equation (8.5). Changing the representation domain is done using the 2-D discrete Fourier transform. Consequently, the input/output relation, in the spatial domain, is no longer described by a simple discrete convolution equation, but by a circular convolution equation. We will look at the effects of this phenomenon at the end of this section.

8.5.1. 2-D discrete Fourier transform (DFT)

Let us look at a sequence of two indices {x_k,l}. To simplify our presentation, we assume that the two indices have the same variation domain, from 0 to N−1. The transformed sequence is given by:

It is clear that the transform sequence is periodic, of period N for each index.

Equation (8.36) also shows that the transformation is separable, being constituted of a discrete 1-D Fourier transform (DFT) operating row by row, followed with a DFT column by column.

As in the 1-D context, the 2-D discrete Fourier transform is inversible:

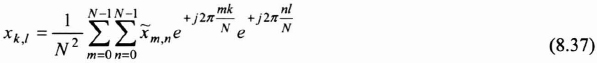
As in the 1-D context, we ...