6.1. Introduction to infinite impulse response filters
Infinite impulse response (IIR) filters are recursive mode filters that are characterized by the following difference equation:
![]()
where at least one of the coefficients {bi}1≤i≤N−1 is non-null. We can easily reduce this to a relation where a0 = 1. From here, we will assume that this hypothesis is satisfied.
Equation (6.1) is verified for all the values of k. We thus have:
![]()
By reinjecting equation (6.2) of y(k − 1) in the difference equation in (6.1), we see that y(k) depends on the preceding values of the output y(k − 2),…, y(k − M) and of N + 1 values of the input signal x(k),…, x(k −N). By repeating this step to infinity, we express the output y(k) as a linear combination of an infinity of terms of the input signal x(k). The filter is therefore an IIR filter.
The z-transform on equation (6.2) helps us obtain the transfer function of the filter, which is a rational fraction in z:
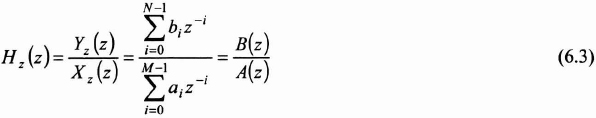
The division following the increasing powers of the numerator by the denominator then leads to an infinite sum of terms.
If the order of a finite impulse response (FIR) filter is between 25 and 400, that of an equivalent IIR filter is generally lower and ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

