5.3. Optimal approach of equal ripple in the stop-band and passband
Finding an optimal solution to the problem of the amplitude approximation of specifications is obtained by minimizing a distance criterion between the theoretical frequency responses and those brought about by synthesis.
To present this approach, we will consider a low-pass linear phase FIR filter of type II (see equations (5.30) and (5.31)); that is, with a symmetrical impulse response and a choice of N odd response.
We then introduce the quantities:
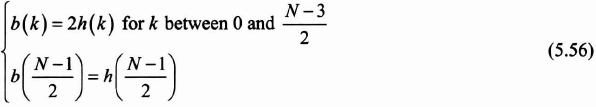
We have seen that in equations (5.30) and (5.31), the related transfer function satisfies the formula:
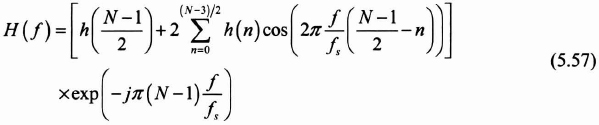
Taking into account equation (5.56), equation (5.57) is written as follows:
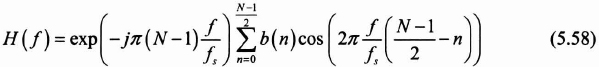
To simplify matters, we only consider the quantity Hr(f), which determines the amplitude:
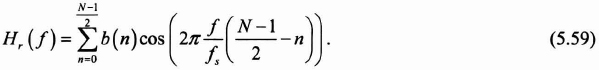
The problem is in estimating the coefficients b(n) so that the frequency response is optimal by distributing the approximation error in the passband and the attenuated band.
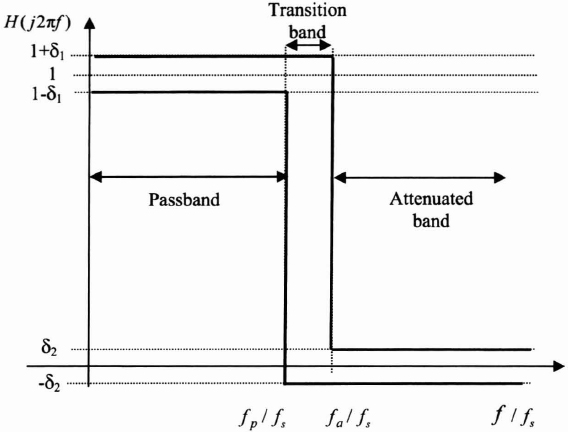
Figure 5.18. Frequency response ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

