3.3. The discrete Fourier transform (DFT)
3.3.1. Expressing the Fourier transform of a discrete sequence
Let us look at the signal xs(t) coming from the sampling of x(t) at the sampling frequency fs:
![]()
According to equation (3.24), the Fourier transform of the signal xs(t) verifies the following relation:
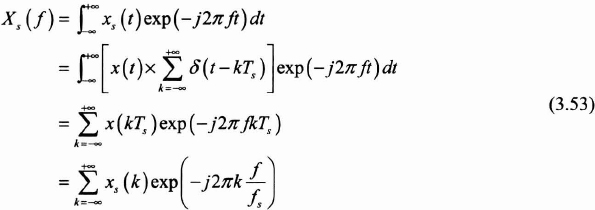
If we introduce fr, the frequency reduced or normalized in relation to the sampling frequency ![]() , we will have:
, we will have:
![]()
The Fourier transform of a discrete sequence is one of the most commonly used spectrum analysis tools. It consists in decomposing the discrete-time signal on an orthonormal base of complex exponential functions.
Xs (fr) is generally a complex function of the reduced frequency fr, as we see in the following expression:
![]()
Among the properties of the Fourier transform, we can first of all consider that:
![]()
Then, using equation (3.54), we have:
Secondly, we can verify that the Fourier ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

