Use Microsoft Excel to plot data distributions so that you can have a better understanding of statistics.
There is some truth to the cliché “a picture is worth a thousand words.” A picture is often the best way to understand 1,000 numbers. People are visually oriented. We’re good at looking at a picture and observing different characteristics; we’re bad at looking at a list of 1,000 numbers.
One of the most powerful tools available for understanding data is the histogram, a picture of the distribution of values. Here is the idea of a histogram. Suppose you have a lot of data—say, the batting averages for all 6,032 baseball players between 1955 and 2004 who averaged 3.1 or more plate appearances per game. Let’s also assume you want to know how these values are distributed. What are the lowest and highest values? Are there more low values than high values? Were batting averages totally random numbers between 0 and .400, or was there some pattern?
Batting average can take many different values. Between 1955 and 2004, 6,032 players had qualifying batting averages, and there were 1,229 unique values for batting average. You can plot the number of players with each unique batting average (though I can’t imagine what this graph would look like). But we don’t really care about each unique value; for example, the fact that 13 players had a batting average of .2862 is not that interesting. Instead, we might want to know the number of players with very similar batting averages—say, between .285 and .290.
Let’s think of each range as a bucket. Every player-season goes into a bucket. For example, in 1959, Hank Aaron had a .354 average, so we’ll put that season in the .350–.355 bucket. So, here’s our plan: we’ll put each player-season into a bucket, count the number of player-seasons in each bucket, and draw a graph showing (in ascending order) the number of players in each bucket. This single diagram is a histogram.
In this example, I wanted to look at the distribution of batting average. I used a table containing the total batting statistics for each player in each year (and the list of all teams for which each player played), and I called the table b_and_t. You can find complete instructions on how to create this table in “Measure Batting with Batting Average” [Hack #40] . I selected only batters with enough plate appearances to qualify for a league title, and only those players who played between 1955 and 2004:
SELECT b.playerID, M.nameLast, M.nameFirst, b.yearID, b.teamG, b.teamIDs, b.AB, b.H, b.H/b.AB AS AVG, b.AB + b.BB + b.HBP + b.SF as PA FROM b_and_t b inner join Master M on b.playerID=m.playerID WHERE yearID > 1954 AND b.AB + b.BB + b.HBP + b.SF > b.teamG * 3.1;
After running this query, I saved the results to an Excel file named batting_averages.xls. For instructions on how to save query results as Excel files, see “Move Data from a Database to Excel” [Hack #19] .
One way to draw histograms in Excel is to use the Analysis ToolPak add-in. You can add this by selecting Add-Ins…from the Tools menu, and then selecting Analysis ToolPak. This adds a new menu item to the Tools menu, called Data Analysis, which introduces several new functions, including a Histogram function. But I find this interface confusing and inflexible, so I do something else.
Here is my method for creating a histogram:
In the data worksheet, create a new column called Range.
In the first cell of this column, use a function to round the value for which you would like to plot the distribution. The simple way to do this is to use the Significant Figures option of the ROUND function. In my worksheet, column I contained the value for which I wanted to calculate the distribution (batting average), so I could use a formula such as ROUND(I2,2) to round to the nearest .010. Personally, I find a bucket size of .005 to be more descriptive, so I use a trick. You can multiply a value inside the ROUND function and then divide outside the function to get buckets of almost any size. Inside the ROUND function, I multiply by the reciprocal of the bucket size—in this case, 1 / .005 = 200. Outside the function, I multiply by the bucket size. In my worksheet, column I contained the average values. So, I used ROUND(I2 * 200,0) / 200 as my formula. Copy and paste this formula into every row of the worksheet. (You can double-click the bottom-right corner of the cell to do this quickly.)
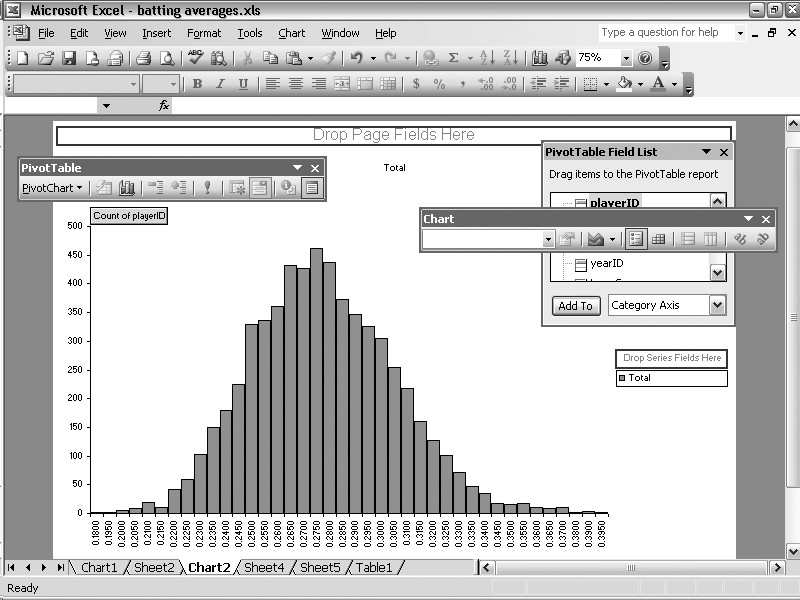
Now, we’re ready to count the number of players in each bucket. Select all of the data in the worksheet, including the new Range column. From the Data menu, select Pivot Table and Pivot Chart Report. Select Pivot Chart Report and click Finish (we’ll use all the defaults). We will select two fields for our pivot table. From the Pivot Table Field List palette, select Range. Drag-and-drop this onto the Drop Row Fields Here part of the pivot table. Next, drag-and-drop “playerID” onto the Drop Data Item Here part of the pivot table. By default, Excel will count the number of player IDs in the underlying data that match each range value. The pivot table is now showing the number of items in each bucket. You should see a (very ugly) graph with the number of players in each bucket.
Clean up the graph. (I like to erase the background fill and lines and change the width of the columns.) Figure 4-1 shows an example of a cleaned-up graph.
Looking at the histogram, we see that the distribution looks similar to a bell curve; it skews toward the right and is centered at around .275.
One of the nice things about calculating bins with formulas is that you can easily change the formula for binning. Here are a few suggestions for other formulas:
- ROUNDDOWN(<value>, <significance>) and ROUNDUP(<value>, <significance>)
This ROUNDDOWN function rounds down to the nearest significant figure. For example, ROUNDDOWN(3.59,0) equals 3, and ROUNDDOWN(3.59,1) equals 3.5. Similarly, ROUNDUP rounds up to the nearest significant figure. ROUNDUP(3.59, 0) equals 4, and ROUNDUP(3.59,1) equals 3.6.
- LOG(<value>, <base>)
Sometimes it’s useful to plot a value on a logarithmic scale, and to use logarithmic-size bins. You can combine LOG functions with ROUND functions to create variable-size bins.
- CONCATENATE(…)
The CONCATENATE function doesn’t compute numbers, it puts text together. If you want to explicitly list ranges (such as 3.500–3.599), you can use the CONCATENATE function to create these; for example, CONCATENATE(ROUNDDOWN(3.59,1),” to “,ROUNDUP(3.59,1)-0.01) returns 3.5 to 3.59.
If you want to take this to the next level, you can replace the bin size with a named value. (For example, name cell A1 bin_size.) This makes it easy to change the bin size dynamically and experiment with different numbers of bins.
Get Baseball Hacks now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.