Maximum Flow
Given a flow network, it is possible to compute the maximum flow (mf) between vertices s and t given the capacity constraints c(u,v)≥0 for all directed edges e=(u,v) in E. That is, compute the largest amount that can flow out of source s, through the network, and into sink t given specific capacity limits on individual edges. Starting with a feasible flow (a flow of 0 through every edge is feasible), Ford-Fulkerson (Figure 8-3) successively locates an augmenting path through the network from s to t to which more flow can be added. The algorithm terminates when no augmenting paths can be found. The Max-flow Min-cut theorem (Ford-Fulkerson, 1962) guarantees that with non-negative flows and capacities, Ford-Fulkerson always terminates and identifies the maximum flow in a network.
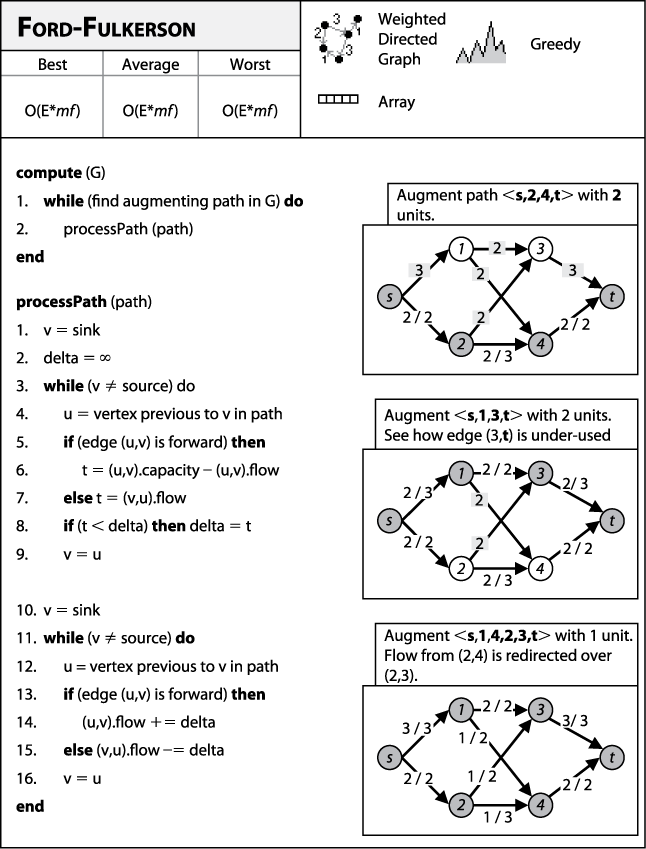
Figure 8-3. Ford-Fulkerson fact sheet
Input/Output
In this presentation, we describe Ford-Fulkerson using linked lists to store edges. Each vertex u maintains two separate lists: forward edges for the edges emanating from u and backward edges for the edges coming into u; thus each edge appears in two lists, doubling the total storage. The code repository provided with this book contains an implementation using a two-dimensional matrix to store edges, a more appropriate data structure to use for dense flow network graphs.
Input
The flow network is defined by a graph G=(V, E) with designated start ...
Get Algorithms in a Nutshell now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

