Before going any further, Gary wanted to get a better understanding of the running profile of programs. He and Graham sat down and wrote some short programs to see how they ran with Graham's custom library linked in. Perhaps they could get a better understanding of the conditions that caused the problem to arise.
Tip
What type of experiments would you run? What would your program(s) look like?
The first test program Gary and Graham wrote (ProgramA) is shown in Example 1-1.
Example 1-1. ProgramA code
int main(int argc, char **argv) {
int i = 0;
for (i = 0; i < 1000000; i++) {
malloc(32);
}
exit (0);
}They ran the program and waited for the results. It took several minutes to finish. Although computers were slower back then, this was clearly unacceptable. When this program finished, there were 32 MB of memory leaks. How would the program run if all of the memory allocations were deallocated? They made a simple modification to create ProgramB, shown in Example 1-2.
Example 1-2. ProgramB code
int main(int argc, char **argv) {
int i = 0;
for (i = 0; i < 1000000; i++) {
void *x = malloc(32);
free(x);
}
exit (0);
}When they compiled and ran ProgramB, it completed in a few seconds. Graham was convinced that the problem was related to the number of memory allocations open when the program ended, but couldn't figure out where the problem occurred. He had searched through his code for several hours and was unable to find any problems. Gary wasn't as convinced as Graham that the problem was the number of memory leaks. He suggested one more experiment and made another modification to the program, shown as ProgramC in Example 1-3, in which the deallocations were grouped together at the end of the program.
Example 1-3. ProgramC code
int main(int argc, char **argv) {
int i = 0;
void *addrs[1000000];
for (i = 0; i < 1000000; i++) {
addrs[i] = malloc(32);
}
for (i = 0; i < 1000000; i++) {
free(addrs[i]);
}
exit (0);
}This program crawled along even slower than the first program! This example invalidated the theory that the number of memory leaks affected the performance of Graham's program. However, the example gave Gary an insight that led to the real problem.
It wasn't the number of memory allocations open at the end of the program that affected performance; it was the maximum number of them that were open at any single time. If memory leaks were not the only factor affecting performance, then there had to be something about the way Graham maintained the information used to determine whether there were leaks. In ProgramB, there was never more than one 32-byte chunk of memory allocated at any point during the program's execution. The first and third programs had one million open allocations. Allocating and deallocating memory was not the issue, so the problem must be in the bookkeeping code Graham wrote to keep track of the memory.
Gary asked Graham how he kept track of the allocated memory. Graham replied that he was using a binary tree where each node was a structure that consisted of pointers to the children nodes (if any), the address of the allocated memory, the size allocated, and the place in the program where the allocation request was made. He added that he was using the memory address as the key for the nodes since there could be no duplicates, and this decision would make it easy to insert and delete records of allocated memory.
Using a binary tree is often more efficient than simply using an ordered linked list of items. If an ordered list of n items exists—and each item is equally likely to be sought—then a successful search uses, on average, about n/2 comparisons to find an item. Inserting into and deleting from an ordered list requires one to examine or move about n/2 items on average as well. Computer science textbooks would describe the performance of these operations (search, insert, and delete) as being O(n), which roughly means that as the size of the list doubles, the time to perform these operations also is expected to double.[2]
Using a binary tree can deliver O(logn) performance for these same operations, although the code may be a bit more complicated to write and maintain. That is, as the size of the list doubles, the performance of these operations grows only by a constant amount. When processing 1,000,000 items, we expect to examine an average of 20 items, compared to about 500,000 if the items were contained in a list. Using a binary tree is a great choice—if the keys are distributed evenly in the tree. When the keys are not distributed evenly, the tree becomes distorted and loses those properties that make it a good choice for searching.
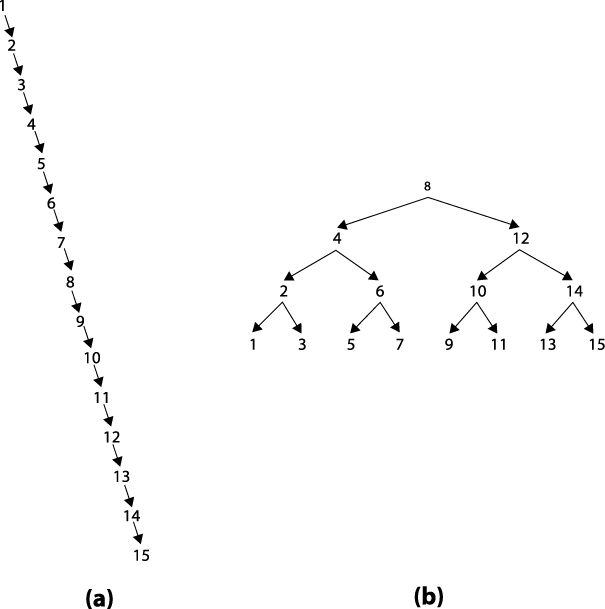
Knowing a bit about trees and how they behave, Gary asked Graham the $64,000 (it is logarithmic, after all) question: "Are you balancing the binary tree?" Graham's response was surprising, since he was a very good software developer. "No, why should I do that? It makes the code a lot more complex." But the fact that Graham wasn't balancing the tree was exactly the problem causing the horrible performance of his code. Can you figure out why? The malloc() routine in C allocates memory (from the heap) in order of increasing memory addresses. Not only are these addresses not evenly distributed, the order is exactly the one that leads to right-oriented trees, which behave more like linear lists than binary trees. To see why, consider the two binary trees in Figure 1-2. The (a) tree was created by inserting the numbers 1-15 in order. Its root node contains the value 1 and there is a path of 14 nodes to reach the node containing the value 15. The (b) tree was created by inserting these same numbers in the order <8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15>. In this case, the root node contains the value 8 but the paths to all other nodes in the tree are three nodes or less. As we will see in Chapter 5, the search time is directly affected by the length of the maximum path.
Algorithms to the Rescue
A balanced binary tree is a binary search tree for which the length of all paths from the root of the tree to any leaf node is as close to the same number as possible. Let's define depth(Li) to be the length of the path from the root of the tree to a leaf node Li. In a perfectly balanced binary tree with n nodes, for any two leaf nodes, L1 and L2, the absolute value of the difference, |depth(L2)-depth (L1)|≤1; also depth(Li)≤log(n) for any leaf node Li.[3] Gary went to one of his algorithms books and decided to modify Graham's code so that the tree of allocation records would be balanced by making it a red-black binary tree. Red-black trees (Cormen et al., 2001) are an efficient implementation of a balanced binary tree in which given any two leaf nodes L1 and L2, depth(L2)/depth(L1)≤2; also depth(Li)≤2*log2(n+1) for any leaf node Li. In other words, a red-black tree is roughly balanced, to ensure that no path is more than twice as long as any other path.
The changes took a few hours to write and test. When he was done, Gary showed Graham the result. They ran each of the three programs shown previously.
ProgramA and ProgramC took just a few milliseconds longer than ProgramB. The performance improvement reflected approximately a 5,000-fold speedup. This is what might be expected when you consider that the average number of nodes to visit drops from 500,000 to 20. Actually, this is an order of magnitude off: you might expect a 25,000-fold speedup, but that is offset by the computation overhead of balancing the tree. Still, the results are dramatic, and Graham's memory leak detector could be released (with Gary's modifications) in the next version of the product.
Get Algorithms in a Nutshell now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.