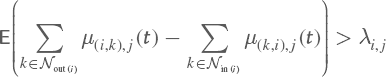• Flows f(k,i),j are all nonnegative and positive flows are not assigned to nonexistent links.
• Packets that have reached the destination are not injected back into the network.
We can show the following lemma.
The following is an informal proof. Recall that any link capacity vector in can be achieved by a stationary randomized schedule that chooses the link ...
Get Wireless Networking Complete now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.