VLSI Digital Signal Processing Systems: Design and Implementation

C.3    EUCLIDEAN GCD ALGORITHM FOR POLYNOMIALS

Theorem C.3.1 (Division Algorithm for Polynomials) For 2 polynomials c(x) and d(x) with d(x) not equal to zero, there is a unique pair of polynomials Q(x) (the quotient polynomial) and r(x) (the remainder polynomial) such that

and deg r(x) < deg d(x).

Theorem C.3.2 (Euclidean GCD Algorithm for Polynomials) Given the polynomials s(x) and r(x) over certain field, their greatest common divisor can be computed by applying iteratively the division algorithm. Suppose deg s(x) ≥ deg r(x) ≥ 0, then this computation is carried out iteratively as:

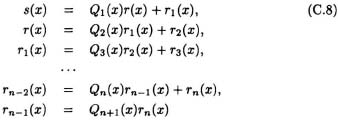
and the process stops when a remainder of zero is obtained. Then

where α is a scalar.

Corollary C.3.1  For any polynomials s(x) and r(x), there exist polynomials a(x) and b(x) such that

The procedure to find the polynomials a(x) and b(x) is the same as that for the integers.

Example C.3.1 Find GCD(s(x),r(x)), given s(x) = x³ − x² + x − 1 and r(x) = x² − 2x + 1. Express GCD(s(x),r(x)) in terms of s(x) and r(x) as in(C.10).

From Euclidean algorithm, we have

Therefore, GCD(s(x), r(x)) = 2(x − 1). By using ...