VLSI Digital Signal Processing Systems: Design and Implementation

C.2    EUCLIDEAN GCD ALGORITHM FOR INTEGERS

Theorem C.2.1 (Division Algorithm) For every pair of integers c and d with d nonzero, there is a unique pair of integers Q (the quotient) and r (the remainder) such that c = dQ + r, where 0 ≤ |r| < |d|.

Using the division algorithm, the GCD of 2 integers can be found.

Example C.2.1 GCD(993,186) can be found as follows:

Since GCD(993,186) divides 993 and 186, it must divide the 1st remainder 63. Because it divides 186 and 63, it must divide the 2nd remainder 60. Because it divides 63 and 60, it divides 3. On the other hand, 3 divides 60, and hence 63, and hence 186 and 993. Therefore, GCD(993,186)=3.

Following is the Euclidean GCD algorithm for integers.

Theorem C.2.2 (Euclidean GCD Algorithm) Given 2 positive integers s and r, their greatest common divisor can be computed by iteratively applying the division algorithm. Suppose r < s, then the algorithm is continued iteratively as shown below:

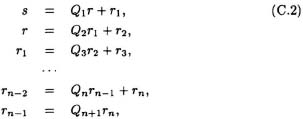
and the process stops whenever the remainder is zero. The last nonzero number, r_n is the greatest common divisor.

Corollary C.2.1  For any positive ...