VLSI Digital Signal Processing Systems: Design and Implementation

9.3    DISCRETE COSINE TRANSFORM AND INVERSE DCT

The discrete cosine transform (DCT) is a frequency transform used in still and moving video compression [13] (see Section 1.2.6). This section addresses fast implementations of DCT based on algorithm-architecture transformations and the decimation-in-frequency approach.

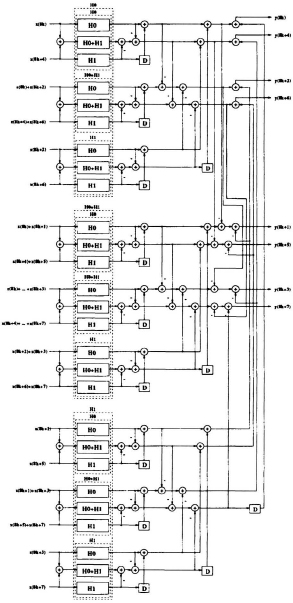
Fig. 9.9    Reduced-complexity 8-parallel FIR filter.

Denote the DCT of the data sequence x(n), n = 0,1, ··· , N − 1, by X(k), k = 0,1, ··· , N − 1. The DCT and inverse DCT (IDCT) algorithms are described by the following equations:

DCT:

and

IDCT:

where

Notice that the DCT is an orthogonal transform, i.e., the transformation matrix for IDCT is a scaled version of the transpose of that for the DCT and vice versa. Therefore, the DCT architecture can be obtained by “transposing” the IDCT, i.e., reversing the direction of the arrows in the flow graph of IDCT, and the IDCT can be obtained by “transposing” the DCT.

It is easy to verify that a direct implementation of DCT or IDCT requires N(N − 1) multiplication operations, i.e., O(N²), which is very hardware expensive. Therefore, ...