7.8 PROBLEMS
- For the DG shown in Fig. 7.24,
(a) Which of the following sets of scheduling and projection are permissible?
i. s = [1 0]T, d = [1 0]T
ii. s = [1 2]T, d = [2 − 1]T
iii. s = [1 1]T, d = [1 0]T
iv. s = [1 − 2]T, d = [1 0]T
(b) Derive the projected systolic array for each permissible set.
- Draw the space-time mapping of design R1.
- Using one or more transformations such as edge reversal, associativity, slow-down, retiming, and pipelining, derive design R1 from B2.
- For the two designs R2 and dual R2, draw the architecture block diagrams and their space-time mappings.
- Using one or more transformations such as edge reversal, associativity, slow-down, retiming, and pipelining, show all steps needed to obtain dual R2 from R2.
- Draw the space-time representation and the systolic architecture of the design W1 with
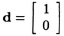 , pT = [ 0 1 ], and sT = [ 2 1 ].
, pT = [ 0 1 ], and sT = [ 2 1 ]. - Derive design W1 from design F using transformations such as edge reversal, associativity, slow-down, retiming, and pipelining.
- For the two designs W2 and dual W2, draw the architecture block diagrams and their space-time mappings. Why are these two architectures dual of each other?
- Consider the DG of a 5-tap convolution filter shown in Fig. 7.25. Assume that the inputs and the coefficients can be broadcast (with no time delay) to all processors simultaneously or can be delayed for fully systolic design. Further assume that ...
Get VLSI Digital Signal Processing Systems: Design and Implementation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

