VLSI Digital Signal Processing Systems: Design and Implementation

13.7    DISTRIBUTED ARITHMETIC

Distributed arithmetic is used to design bit-level architectures for vector-vector multiplications. In distributed arithmetic, each word in the vectors is represented as a binary number, the multiplications are reordered and mixed such that the arithmetic becomes “distributed” through the structure. Distributed arithmetic is commonly used for implementation of convolution operations and discrete cosine transforms (DCT) commonly used in video compression systems [17],[18].

13.7.1    Conventional Distributed Arithmetic

Consider an inner product between 2 length-N vectors C and X:

where {c_i}’s are M-bit constants and {x_i}’s are coded as W-bit 2’s complement numbers

Substituting (13.21) in (13.20),

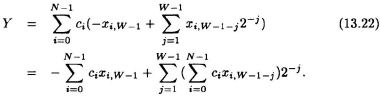
Define

Then,

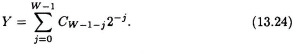
Therefore, by interchanging the summing order of i and j, the initial multiplications in (13.20) are now distributed to another computation pattern [19], [20].

Since the term C_j depends on the x_i,j values and has only 2^N possible values, it is possible ...