13.2 PARALLEL MULTIPLIERS
This section considers multipliers that can perform two’s complement multiplication in time O(W) using regular structures, including multiplication with sign extension (derived from Horner’s rule) and Baugh-Wooley multiplication [9]. Two regular implementation styles, carry-ripple and and carry-save array, are introduced.
It has been proved that multiplications cannot be performed in a time smaller than O(log2W). Such a bound is attainable by the binary-tree and Wallace-tree multipliers (see Appendix E) [10]. However, their corresponding architectures are very irregular.
Let the multiplicand and multiplier be A and B:
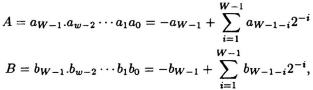
where −1 < A, B < 1 and the case when both A and B is equal to −1 is excluded. The value of their product P = A × B is given by:
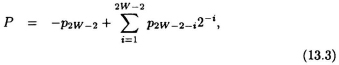
where the radix point is to the right of the msb p2w−2. Since the product of 2 numbers within [−1, 1) is also in this range, all higher order bits to the left of bit-position 2W − 2 in the result are ignored.
In constant wordlength multiplication, the W − 1 lower order bits in the product P are discarded, and the product is denoted as X ⇐ P = A × B, where
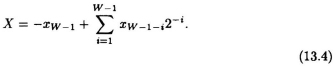
The product X is used when a constant wordlength multiplier ...
Get VLSI Digital Signal Processing Systems: Design and Implementation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

