11.4 SCALING AND ROUNDOFF NOISE COMPUTATION
11.4.1 Scaling Operation
As mentioned before, the same wordlength can be assigned to all the variables of the system only if all the states have equal power. The way to achieve this is called scaling. The state vector is premultiplied by inverse of the scaling matrix T. If we denote the scaled states by xs, we can write,
![]()
Substituting for x from (11.29) into the state update equation (11.10) and solving for xs we get,
![]()
![]()
![]()
where As = T−1AT and bs = T−1b.
Similarly the output equation (11.11) can be derived as follows,
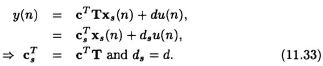
The scaled K matrix is given by
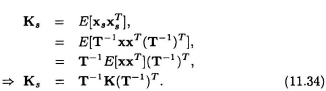
Since it is desirable to have equal power at all states, a transformation matrix T is chosen such that the Ks matrix of the scaled system has all diagonal entries as 1. Further assume T to be diagonal, i.e.,
From (11.34) we can write the diagonal entries of Ks in terms of those of K
Fig. 11.7 ...
Get VLSI Digital Signal Processing Systems: Design and Implementation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

