Chapter 2. Descriptive Statistics
Means and Averages
In the previous chapter, I mentioned three summary statistics—mean, variance, and median—without explaining what they are. So before we go any farther, let’s take care of that.
If you have a sample of n values, xi, the mean, μ, is the sum of the values divided by the number of values; in other words
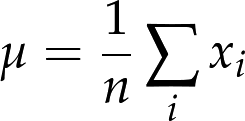
The words “mean” and “average” are sometimes used interchangeably, but I will maintain this distinction:
The “mean” of a sample is the summary statistic computed with the previous formula.
An “average” is one of many summary statistics you might choose to describe the typical value or the central tendency of a sample.
Sometimes the mean is a good description of a set of values. For example, apples are all pretty much the same size (at least the ones sold in supermarkets). So if I buy six apples and the total weight is three pounds, it would be reasonable to conclude that they are about a half pound each.
But pumpkins are more diverse. Suppose I grow several varieties in my garden, and one day I harvest three decorative pumpkins that are one pound each, two pie pumpkins that are three pounds each, and one Atlantic Giant pumpkin that weighs 591 pounds. The mean of this sample is 100 pounds, but if I told you “The average pumpkin in my garden is 100 pounds,” that would be wrong, or at least misleading.
In this example, there is no meaningful average ...
Get Think Stats now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

