4.4 NON CONTEXT FREE LANGUAGES; ANOTHER PUMPING LEMMA
In this section we prove a pumping lemma for CFL that is similar, but as expected from the richer structure of the PDA, more complex than the one for regular languages. We will benefit in our proof from the concept of parse tree for a CFG. The reader has most likely encountered trees in courses on discrete mathematics, data structures, etc. A tree is a structure like the one drawn below:
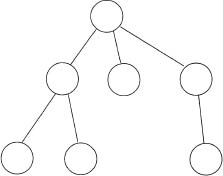
Since by default all edges point “downwards”, one does not need to emphasize so by drawing them as arrows. The round nodes may or may not have names. Our parse trees will have all their nodes named. The precise angle or slope of the edges does not matter—meaning, we allow variation in drawings without changing the tree we want to depict. However, left to right order matters, thus the following is a different tree from the one above. Our trees are ordered.
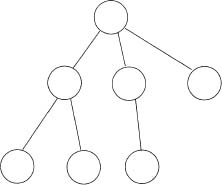
Of course, the reader has encountered many aspects of discrete mathematics before, but this did not stop me from reintroducing some such concepts in Chapter 1. So, let us revisit the definition of trees. A tree has both a “data” component (the node “contents”, whatever they may be) and a structural component or geometry, that is, how the nodes are interconnected. This motivates us to opt for ...
Get Theory of Computation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

