3.5 ADDITIONAL EXERCISES
- Describe in set-theoretic notation the language of the automaton in 3.1.2.4. Independently, describe set-theoretically the complement {0n 1 : n ≥ 0} and verify that your two answers are equivalent.
- Construct a FA M over A = {0, 1} such that L(M) = {
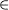 }
} - Construct a FA M over A = {0, 1} such that L(M) = {0, 1}+, that is, L(M) = A* − {
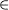 }.
}. - Construct a FA that accepts L = {00, 11, 10} over A = {0, 1}.
- Let Σ = {0}. Which of the following languages over Σ is regular, and why?
(a) {x : |xx| is odd}
(b) {x : |x| is odd}
(c) {x : |xx| is not a prime}
(d) {x : |x| is not a prime}
(e) {x : |x| is a perfect cube}
- Find a finite automaton that accepts the language over A = {0, 1} that contains precisely the strings that have no three consecutive 0s.
- Find a finite automaton that accepts the language over A = {0, 1} that contains precisely the strings that end in precisely three consecutive 0s.
- Find a finite automaton that accepts the language over A = {0, 1} that contains precisely the strings that end in at least three consecutive 0s.
- Design a FA over {0, 1} that accepts exactly all the strings of length 3k + 1 for some natural number k.E.g., 0, 0110, 0000 are all in. 00, 000, 01101 are not.
- Build a NFA that accepts precisely all the strings over {0, 1} of length ≥ 5 that ...
Get Theory of Computation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

