3.1 DETERMINISTIC FINITE AUTOMATA AND THEIR LANGUAGES
3.1.0.6 Example. Consider the restricted URM below that operates over the input alphabet {0, 1}

What does this program do? It has scanned a string of parity 0 (sum of its digits is even) and halted iff it halted while in state 0. This claim will be revisited after we formalize the automaton concept. ![]()
3.1.1 The Flow-Diagram Model
The formalization is achieved by first abstracting a command
![]()
as the configuration below:
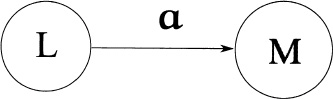
Figure capturing (1) above
Thus the “read” part is implicit, while the labeled arrow that connects the states L and M denotes exactly the semantics of (1). Therefore, an entire automaton is a directed graph—that is, a finite set of (possibly) labeled circles, the states, and a finite set of arrows, the transitions, the latter labeled by members of the automaton’s input alphabet. The arrows or edges interconnect the states. If L = M, then we have the configuration
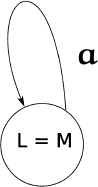
where the optional label could be L, or M, L = M (as ...
Get Theory of Computation now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

