The Mathematics of Derivatives: Tools for Designing Numerical Algorithms

CHAPTER 5

From Stochastic Processes Formalism to Differential Equation Formalism

5.1. BACKWARD AND FORWARD KOLMOGOROV EQUATIONS

In this section no results will be derived per se. Some results, however, relevant to our topic will be stated.

Given a generalized price process,

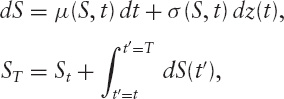
with arbitrary drift function and local volatility function, we may ask the following questions:

• Given that we start at stock price S_t at time t, what is the probability distribution over S_T at some time T > t?
• What are the ending expectation values of observables (i.e., expectation values of functions of the path end-point or state variable)?
• What are the expectation values of these observables as functions of the path start-points S_t ?

It turns out that a probability distribution exists P(S_t, S_T), which encapsulates all this and satisfies two equations (of motion) in the two sets of variables. The first is called the Fokker-Planck (also called the forward Kolmogorov) equation:

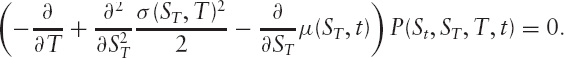
(Note: As a reminder, this operator notation implies that the derivative operators act on everything to the right.) The second is the backward Kolmogorov equation:

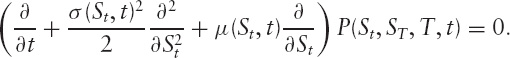
For example, for a constant mean and standard deviation µ₀, σ₀, that ...