15.3. The Sine Wave as a Function of Time
In our graphs of the sine wave so far, we have plotted y as the function of an angle. The units on the horizontal axis have been degrees or radians. But for many applications we have a periodic function that varies with time, rather than an angle. For example, an alternating voltage varies with time, so many cycles per second. The same is true of mechanical vibrations and other periodic phenomena. Fortunately we can rewrite all our previous definitions and formulas in terms of time.
The sine curve can be generated in a simple geometric way. Figure 15-12 shows a vector OP rotating counterclockwise with a constant angular velocity ω. A rotating vector is called a phasor. Its angular velocity ω is almost always given in radians per second (rad/s).
Figure 15.12. The sine curve generated by a rotating vector.
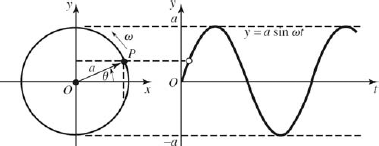
If the length of the phasor is a, then its projection on the y axis is
- y = a sin θ
But since the angle θ at any instant t is equal to ωt,
- y = a sin ωt
Further, if the phasor does not start from the x axis but has some phase angle ϕ we get
- y = a sin(ωt + ϕ
Notice in this equation that y is a function of time, rather than of an angle.
Example 12:Write the equation for a sine wave generated by a phasor of length 8 rotating with an angular velocity of 300 rad/s and with a phase angle of 0. Solution: Substituting, with a = 8, ω = 300 rad/s, ... |
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

