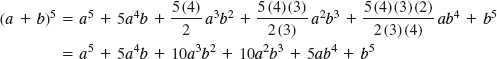20.5. The Binomial Theorem
20.5.1. Powers of a Binomial
Recall that a binomial, such as (a + b), is a polynomial with two terms. By actual multiplication we can show that
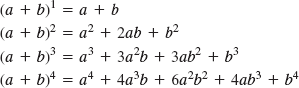
We now want a formula for (a + b)n with which to expand a binomial without actually carrying out the multiplication. In the expansion of (a + b)n, where n is a positive integer, we note the following patterns:
There are n + 1 terms.
The power of a is n in the first term, decreases by 1 in each later term, and reaches 0 in the last term.
The power of b is 0 in the first term, increases by 1 in each later term, and reaches n in the last term.
Each term has a total degree of n. (That is, the sum of the degrees of the variables is n.)
The first coefficient is 1.
The product of the coefficient of any term and its power of a, divided by the number of the term, gives the coefficient of the next term. (This property gives a recursion formula for the coefficients of the binomial expansion.)
These six observations can be expressed as the formula:
![]()
Example 40:Use the binomial theorem to expand (a + b)5. Solution: From the binomial theorem,
which can be verified by actual multiplication, as shown in the screen. |
TI-89 solution ...
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.