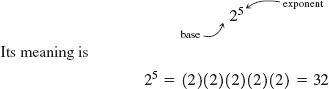2.3. Laws of Exponents
2.3.1. Definitions
We have done some work with powers of numbers in Chapter 1. Now we will expand those ideas to include powers of algebraic expressions. Here we will deal only with expressions that have integers (positive or negative, and zero) as exponents. We will need the laws of exponents to multiply and divide algebraic expressions in the following sections.
Recall from Chapter 1 that a positive exponent shows how many times the base is to be multiplied by itself.
Example 32:In the expression 25, the base is 2 and the exponent is 5.
|
In general,
NOTE

NOTE
An exponent applies only to the symbol directly in front of it.
Thus,
- 5y3 = 5(y3)
but
- 5y3 ≠ 53y3
2.3.2. Multiplying Powers
▪ Exploration:
Try this. (a) Use Eq. 21 to expand x3 into its factors, that is, (x)(x)(x). (b) Similarly expand x4 into its factors. (c) Form the product of x3 and x4, with each in its factored form. (d) Simplify your expression and use Eq. 21 again to write your result as x raised to a power.
What did you find? Can you express your findings as a rule?
You should have found that the exponent in the product is the sum of the two original exponents.
- x3 · x4 = x3+4 = x7
This gives our first law of exponents.
NOTE
Example 33:Here we show the use of Eq. 21.
|
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.