CHAPTER 10
CHAPTER 10 SOLUTIONS
10.1 SECTION 10.2
10.1 When three observations are taken without replacement, there are only four possible results. They are 1,3,5; 1,3,9; 1,5,9; and 3,5,9. The four sample means are 9/3, 13/3, 15/3, and 17/3. The expected value (each has probability 1/4) is 54/12 or 4.5, which equals the population mean. The four sample medians are 3, 3, 5, and 5. The expected value is 4, and so the median is biased.
10.2
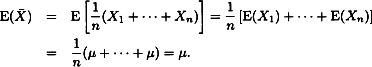
10.3 For a sample of size 3 from a continuous distribution, the density function of the median is 6ƒ(x)F(x)[1 − F(x)]. For this exercise, F(x) = (x − θ + 2)/4, θ − 2 < x < θ + 2. The density function for the median is
![]()
and the expected value is
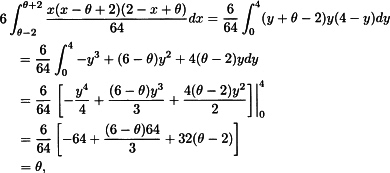
where the first line used the substitution y = x − θ + 2.
10.4 Because the mean of a Pareto distribution does not always exist, it is not reasonable to discuss unbiasedness or consistency. Had the problem been restricted to Pareto distributions with α > 1, then consistency can be established. It turns out that for the sample mean to be consistent, only the first moment needs to exist (the variance having a limit of zero is a sufficient, but not a necessary, condition for consistency).
10.5 The mean ...
Get Student Solutions Manual to Accompany Loss Models: From Data to Decisions, Fourth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

