CHAPTER 9
CHAPTER 9 SOLUTIONS
9.1 SECTION 9.1
9.1 The number of claims, N, has a binomial distribution with m = number of policies and q = 0.1. The claim amount variables, X1, X2,…, all are discrete with Pr(Xj = 5,000) = 1 for all j.
9.2 (a) An individual model is best because each insured has a unique distribution. (b) A collective model is best because each malpractice claim has the same distribution and there are a random number of such claims. (c) Each family can be modeled with a collective model using a compound frequency distribution. There is a distribution for the number of family members and then each family member has a random number of claims.
9.2 SECTION 9.2
9.3
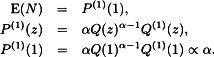
9.4 The Poisson and all compound distributions with a Poisson primary distribution have a pgf of the form P(z) = exp{λ[P2(z) − 1]} = [Q(z)]λ, where Q(z) = exp[P2(z) − 1].
The negative binomial and geometric distributions and all compound distributions with a negative binomial or geometric primary distribution have P(z) = {1 − β[P2(z) − 1]}−r = [Q(z)]r, where Q(z) = {1 − β[P2(z) − 1]}−1.
The same is true for the binomial distribution and binomial-X compound distributions with α = m and Q(z) = 1 + q[P2(z) − 1].
The zero-truncated and zero-modified distributions cannot be written in this form.
9.3 SECTION 9.3
9.5 To simplify writing the expressions, let
and similarly for S. For the first moment, , and ...
Get Student Solutions Manual to Accompany Loss Models: From Data to Decisions, Fourth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

