CHAPTER 4
CHAPTER 4 SOLUTIONS
4.1 SECTION 4.2
4.1 Arguing as in the examples,
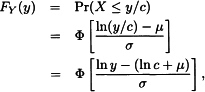
which indicates that Y has the lognormal distribution with parameters μ + ln c and σ. Because no parameter was multiplied by c, there is no scale parameter. To introduce a scale parameter, define the lognormal distribution function as ![]() . Note that the new parameter v is simply eμ. Then, arguing as before,
. Note that the new parameter v is simply eμ. Then, arguing as before,
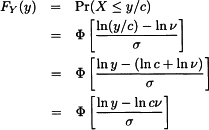
demonstrating that v is a scale parameter.
4.2 The following is not the only possible set of answers to this question. Model 1 is a uniform distribution on the interval 0 to 100 with parameters 0 and 100. It is also a beta distribution with parameters a = 1, b = 1, and θ = 100. Model 2 is a Pareto distribution with parameters α = 3 and θ = 2000. Model 3 would not normally be considered a parametric distribution. However, we could define a parametric discrete distribution with arbitrary probabilities at 0, 1, 2, 3, and 4 being the parameters. Conventional usage would not accept this as a parametric distribution. Similarly, Model 4 is not a standard parametric distribution, but we could define one as having arbitrary probability p at zero and an exponential distribution elsewhere. Model 5 could be from ...
Get Student Solutions Manual to Accompany Loss Models: From Data to Decisions, Fourth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

