Statistical Inference for Models with Multivariate t-Distributed Errors

CHAPTER 3

LOCATION MODEL

Outline

3.1 Model Specification

3.2 Unbiased Estimates of θ and σ² and Test of Hypothesis

3.3 Estimators

3.4 Bias and MSE Expressions of the Location Estimators

3.5 Various Estimates of Variance

3.6 Problems

In this chapter, we discuss some basic results on the location model under the assumption that the error-vector is distributed according to the multivariate t-distribution.

3.1 Model Specification

Consider the location model with the response vector Y = (Y₁, ···, Y_n)′ such that it satisfies the relation

(3.1.1)

where 1_n = (1, ···, 1)′ is an n-tuple of 1’s, and the error vector ε follows the multivariate M⁽ⁿ⁾_t(0, σ²V_n γ_o) with pdf

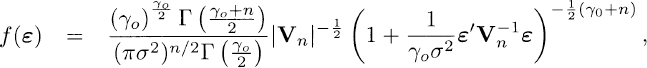
where σ > 0, V_n is a positive definite matrix of rank n and γ_o > 2.

The mean of ε is the zero-vector and the covariance-matrix of ε is

(3.1.2)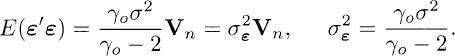

The plan of this chapter is as follows. In sections 2 and 3, unbiased estimators of θ and σ²_ε are proposed along with the test statistic for testing the hypothesis H₀ : θ = θ₀. In addition, we propose some improved estimates of location parameter. Section 4 contains some important theorems for the bias and MSE expressions of the proposed estimators of θ and their mathematical characteristics. ...