Statistical Inference: A Short Course

8.4 A Confidence Interval For The Population Mean μ (σ Unknown)

In the discussion that follows, we shall assume that we are sampling from a normal population. We determined above that a confidence interval for the population mean μ is when σ is known. But if σ is unknown, it must be estimated by

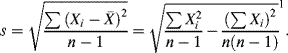
Additionally, if n is “small” , then the statistic

(8.10)

follows a t distribution withdegrees of freedom. So once s replaces σ and n is small, the resulting statistic [Eq. (8.10)] is no longer N(0, 1).

Let us examine the properties of the sampling distribution of the t statistic [Eq. (8.10)]:

1. It is symmetrical about a mean of zero and asymptotic to the horizontal axis.

2. There is a different t distribution for each sample size, that is, t varies with . This dependency on is termed degrees ...