SciPy and NumPy are great tools and provide us with most of the functionality that we need.
Sometimes, though we need more advanced tools, and thatâs where the scikits come in. These are a
set of packages that are complementary to SciPy. There are currently more than 20 scikit
packages available; a list can be found at SciKits. Here we will go over two well-maintained and popular packages: Scikitimage,
a more beefed-up image module than scipy.ndimage, is aimed to
be an imaging processing toolkit for SciPy. Scikit-learn is a machine learning package that can
be used for a range of scientific and engineering purposes.
SciPyâs ndimage class contains
many useful tools for processing multi-dimensional data, such as basic
filtering (e.g., Gaussian smoothing), Fourier transform, morphology (e.g.,
binary erosion), interpolation, and measurements. From those functions we
can write programs to execute more complex operations. Scikit-image has
fortunately taken on the task of going a step further to provide more
advanced functions that we may need for scientific research. These
advanced and high-level modules include color space conversion, image
intensity adjustment algorithms, feature detections, filters for
sharpening and denoising, read/write capabilities, and more.
A common application in imaging science is segmenting image components from one another, which is referred to as thresholding. The classic thresholding technique works well when the background of the image is flat. Unfortunately, this situation is not the norm; instead, the background visually will be changing throughout the image. Hence, adaptive thresholding techniques have been developed, and we can easily utilize them in scikit-image. In the following example, we generate an image with a non-uniform background that has randomly placed fuzzy dots throughout (see Figure 4-1). Then we run a basic and adaptive threshold function on the image to see how well we can segment the fuzzy dots from the background.
Figure 4-1. Illustration of thresholding. The original synthetic image is on the left, with classic and dynamic threshold algorithms at work from middle to right, respectively
# Source code available: scikits_411_ex1.pyimportnumpyasnpimportmatplotlib.pyplotaspltimportscipy.ndimageasndimageimportskimage.filterasskif# Generating data points with a non-uniform backgroundx=np.random.uniform(low=0,high=100,size=20).astype(int)y=np.random.uniform(low=0,high=100,size=20).astype(int)# Creating image with non-uniform backgroundfunc=lambdax,y:x**2+y**2grid_x,grid_y=np.mgrid[-1:1:100j,-2:2:100j]bkg=func(grid_x,grid_y)bkg=bkg/np.max(bkg)# Creating pointsclean=np.zeros((100,100))clean[(x,y)]+=5clean=ndimage.gaussian_filter(clean,3)clean=clean/np.max(clean)# Combining both the non-uniform background# and pointsfimg=bkg+cleanfimg=fimg/np.max(fimg)# Defining minimum neighboring size of objectsblock_size=3# Adaptive threshold function which returns image# map of structures that are different relative to# backgroundadaptive_cut=skif.threshold_adaptive(fimg,block_size,offset=0)# Global thresholdglobal_thresh=skif.threshold_otsu(fimg)global_cut=fimg>global_thresh# Creating figure to highlight difference between# adaptive and global threshold methodsfig=plt.figure(figsize=(8,4))fig.subplots_adjust(hspace=0.05,wspace=0.05)ax1=fig.add_subplot(131)ax1.imshow(fimg)ax1.xaxis.set_visible(False)ax1.yaxis.set_visible(False)ax2=fig.add_subplot(132)ax2.imshow(global_cut)ax2.xaxis.set_visible(False)ax2.yaxis.set_visible(False)ax3=fig.add_subplot(133)ax3.imshow(adaptive_cut)ax3.xaxis.set_visible(False)ax3.yaxis.set_visible(False)fig.savefig('scikits_411_ex1.pdf',bbox_inches='tight')
In this case, as shown in Figure 4-1, the adaptive thresholding technique (right panel) obviously works far better than the basic one (middle panel). Most of the code above is for generating the image and plotting the output for context. The actual code for adaptively thresholding the image took only two lines.
Approaching a slightly different problem, but with a similar setup as before, how can we
identify points on a non-uniform background to obtain their pixel coordinates? Here we can
use skimage.morphology.is_local_maximum, which only needs
the image as a default input. The function works surprisingly well; see Figure 4-2, where the identified maxima are
circled in blue:
# Source code available: scikits_412_ex1.pyimportnumpyasnpimportscipy.ndimageasndimageimportskimage.morphologyasmorphimportmatplotlib.pyplotasplt# Generating data points with a non-uniform backgroundx=np.random.uniform(low=0,high=200,size=20).astype(int)y=np.random.uniform(low=0,high=400,size=20).astype(int)# Creating image with non-uniform backgroundfunc=lambdax,y:np.cos(x)+np.sin(y)grid_x,grid_y=np.mgrid[0:12:200j,0:24:400j]bkg=func(grid_x,grid_y)bkg=bkg/np.max(bkg)# Creating pointsclean=np.zeros((200,400))clean[(x,y)]+=5clean=ndimage.gaussian_filter(clean,3)clean=clean/np.max(clean)# Combining both the non-uniform background# and pointsfimg=bkg+cleanfimg=fimg/np.max(fimg)# Calculating local maximalm1=morph.is_local_maximum(fimg)x1,y1=np.where(lm1.T==True)# Creating figure to show local maximum detection# rate successfig=plt.figure(figsize=(8,4))ax=fig.add_subplot(111)ax.imshow(fimg)ax.scatter(x1,y1,s=100,facecolor='none',edgecolor='#009999')ax.set_xlim(0,400)ax.set_ylim(0,200)ax.xaxis.set_visible(False)ax.yaxis.set_visible(False)fig.savefig('scikits_412_ex1.pdf',bbox_inches='tight')
If you look closely at the figure, you will notice that there are
identified maxima that do not point to fuzzy sources but instead to the
background peaks. These peaks are a problem, but by definition this is
what skimage.morphology.is_local_maximum will find.
How can we filter out these âfalse positivesâ? Since we have the
coordinates of the local maxima, we can look for properties that will
differentiate the sources from the rest. The background is relatively
smooth compared to the sources, so we could differentiate them easily by
standard deviation from the peaks to their local neighboring
pixels.
How does scikit-image fare with real-world research problems? Quite well, in fact. In
astronomy, the flux per unit area received from stars can be measured in images by
quantifying intensity levels at their locationsâa process called photometry. Photometry has
been done for quite some time in multiple programming languages, but there is no de facto
package for Python yet. The first step in photometry is identifying the stars. In the
following example, we will use is_local_maximum to
identify sources (hopefully stars) in a stellar cluster called NGC 3603 that was observed
with the Hubble Space Telescope. Note that one additional package, PyFITS, is used
here. It is a standard astronomical package for loading binary data stored in FITS format:
# Source code available: scikits_412_ex1.pyimportnumpyasnpimportpyfitsimportskimage.morphologyasmorphimportskimage.exposureasskieimportmatplotlib.pyplotasplt# Loading astronomy image from an infrared space telescopeimg=pyfits.getdata('stellar_cluster.fits')[500:1500,500:1500]# Prep file scikit-image environment and plottinglimg=np.arcsinh(img)limg=limg/limg.max()low=np.percentile(limg,0.25)high=np.percentile(limg,99.5)opt_img=skie.exposure.rescale_intensity(limg,in_range=(low,high))# Calculating local maxima and filtering out noiselm=morph.is_local_maximum(limg)x1,y1=np.where(lm.T==True)v=limg[(y1,x1)]lim=0.5x2,y2=x1[v>lim],y1[v>lim]# Creating figure to show local maximum detection# rate successfig=plt.figure(figsize=(8,4))fig.subplots_adjust(hspace=0.05,wspace=0.05)ax1=fig.add_subplot(121)ax1.imshow(opt_img)ax1.set_xlim(0,img.shape[1])ax1.set_ylim(0,img.shape[0])ax1.xaxis.set_visible(False)ax1.yaxis.set_visible(False)ax2=fig.add_subplot(122)ax2.imshow(opt_img)ax2.scatter(x2,y2,s=80,facecolor='none',edgecolor='#FF7400')ax2.set_xlim(0,img.shape[1])ax2.set_ylim(0,img.shape[0])ax2.xaxis.set_visible(False)ax2.yaxis.set_visible(False)fig.savefig('scikits_412_ex2.pdf',bbox_inches='tight')
The skimage.morphology.is_local_maximum function
returns over 30,000 local maxima in the image, and many of the
detections are false positives. We apply a simple threshold value to get
rid of any maxima peaks that have a pixel value below 0.5 (from the
normalized image) to bring that number down to roughly 200. There are
much better ways to filter out non-stellar maxima (e.g., noise), but we
will still stick with the current method for simplicity. In Figure 4-3 we can see that
the detections are good overall. Once we know where the stars are, we
can apply flux measurement algorithms, but that goes beyond the scope of
this chapter.
Figure 4-3. Stars (orange circles) in a Hubble Space Telescope image of a stellar cluster,
identified using the is_local_maximum function
Hopefully, with this brief overview of what is available in the scikit-image package, you already have a good idea of how it can be used for your objectives.
Possibly the most extensive scikit is scikit-learn. It is an easy-to-use machine learning bundle that contains a collection of tools associated with supervised and unsupervised learning. Some of you may be asking, âSo what can machine learning help me do that I could not do before?â One word: predictions.
Let us assume that we are given a problem where there is a good sample of empirical data at hand: can predictions be made about it? To figure this out, we would try to create an analytical model to describe the data, though that does not always work due to complex dependencies. But what if you could feed that data to a machine, teach the machine what is good and bad about the data, and then let it provide its own predictions? That is what machine learning is. If used right, it can be very powerful.
Not only is the scikit-learn package impressive, but its documentation is generous and well organized. Rather than reinventing the wheel to show what scikit-learn is, Iâm going to take several examples that we did in prior sections and see if scikit-learn could provide better and more elegant solutions. This method of implementing scikit-learn is aimed to inspire you as to how the package could be applied to your own research.
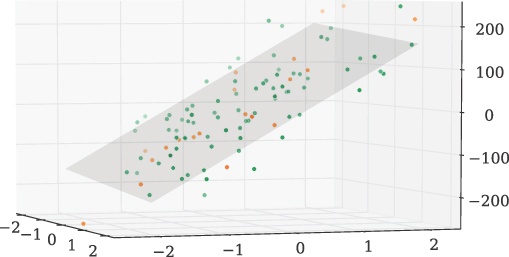
In Chapter 3 we fitted a line to a dataset, which is a linear regression problem. If we are dealing with data that has a higher number of dimensions, how do we go about a linear regression solution? Scikit-learn has a large number of tools to do this, such as Lasso and ridge regression. For now we will stick with the ordinary least squares regression function, which solves mathematical problems of the form
where w is the set of coefficients. The number of coefficients
depends on the number of dimensions in the data, N(coeff) =
MD â 1, where M > 1 and is an integer. In the
example below we are computing the linear regression of a plane in 3D space, so there are
two coefficients to solve for. Here we show how to use LinearRegression to train the model with data, approximate a best fit, give a
prediction from the data, and test other data (test) to
see how well it fits the model. A visual output of the linear regression is shown in Figure 4-4:
# Source code available: scikits_421_ex1.pyimportnumpyasnpfromsklearnimportlinear_modelfromsklearn.datasets.samples_generatorimportmake_regressionimportmatplotlib.pyplotaspltfrommpl_toolkits.mplot3dimportAxes3D# Generating synthetic data for training and testingX,y=make_regression(n_samples=100,n_features=2,n_informative=1,random_state=0,noise=50)# X and y are values for 3D space. We first need to train# the machine, so we split X and y into X_train, X_test,# y_train, and y_test. The *_train data will be given to the# model to train it.X_train,X_test=X[:80],X[-20:]y_train,y_test=y[:80],y[-20:]# Creating instance of modelregr=linear_model.LinearRegression()# Training the modelregr.fit(X_train,y_train)# Printing the coefficients(regr.coef_)# [-10.25691752 90.5463984 ]# Predicting y-value based on trainingX1=np.array([1.2,4])(regr.predict(X1))# 350.860363861# With the *_test data we can see how the result matches# the data the model was trained with.# It should be a good match as the *_train and *_test# data come from the same sample. Output: 1 is perfect# prediction and anything lower is worse.(regr.score(X_test,y_test))# 0.949827492261fig=plt.figure(figsize=(8,5))ax=fig.add_subplot(111,projection='3d')# Dataax.scatter(X_train[:,0],X_train[:,1],y_train,facecolor='#00CC00')ax.scatter(X_test[:,0],X_test[:,1],y_test,facecolor='#FF7800')# Function with coefficient variablescoef=regr.coef_line=lambdax1,x2:coef[0]*x1+coef[1]*x2grid_x1,grid_x2=np.mgrid[-2:2:10j,-2:2:10j]ax.plot_surface(grid_x1,grid_x2,line(grid_x1,grid_x2),alpha=0.1,color='k')ax.xaxis.set_visible(False)ax.yaxis.set_visible(False)ax.zaxis.set_visible(False)fig.savefig('scikits_421_ex1.pdf',bbox='tight')
This LinearRegression function can work with much
higher dimensions, so dealing with a larger number of inputs in a model is straightforward.
It is advisable to look at the other linear regression
models as well, as they may be more appropriate for your data.
SciPy has two packages for cluster analysis with vector quantization (kmeans) and hierarchy. The kmeans method was the easier of the two for implementing and segmenting data
into several components based on their spatial characteristics. Scikit-learn provides a
set of
tools to do more cluster analysis that goes beyond what SciPy has. For a suitable
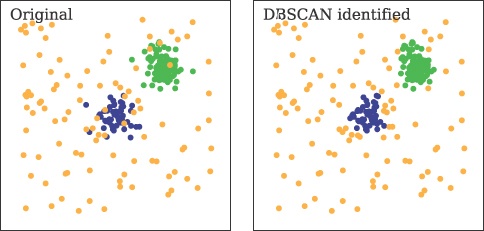
comparison to the kmeans function in SciPy, the DBSCAN algorithm is used in the following example. DBSCAN works by finding core points that have many data points
within a given radius. Once the core is defined, the process is iteratively computed until
there are no more core points definable within the maximum radius? This algorithm does
exceptionally well compared to kmeans where there is
noise present in the data:
# Source code available: scikits_422_ex1.pyimportnumpyasnpfromsklearn.clusterimportDBSCANimportmatplotlib.pyplotasplt# Creating datac1=np.random.randn(100,2)+5c2=np.random.randn(50,2)# Creating a uniformly distributed backgroundu1=np.random.uniform(low=-10,high=10,size=100)u2=np.random.uniform(low=-10,high=10,size=100)c3=np.column_stack([u1,u2])# Pooling all the data into one 150 x 2 arraydata=np.vstack([c1,c2,c3])# Calculating the cluster with DBSCAN function.# db.labels_ is an array with identifiers to the# different clusters in the data.db=DBSCAN().fit(data,eps=0.95,min_samples=10)labels=db.labels_# Retrieving coordinates for points in each# identified core. There are two clusters# denoted as 0 and 1 and the noise is denoted# as -1. Here we split the data based on which# component they belong to.dbc1=data[labels==0]dbc2=data[labels==1]noise=data[labels==-1]# Setting up plot detailsx1,x2=-12,12y1,y2=-12,12fig=plt.figure()fig.subplots_adjust(hspace=0.1,wspace=0.1)ax1=fig.add_subplot(121,aspect='equal')ax1.scatter(c1[:,0],c1[:,1],lw=0.5,color='#00CC00')ax1.scatter(c2[:,0],c2[:,1],lw=0.5,color='#028E9B')ax1.scatter(c3[:,0],c3[:,1],lw=0.5,color='#FF7800')ax1.xaxis.set_visible(False)ax1.yaxis.set_visible(False)ax1.set_xlim(x1,x2)ax1.set_ylim(y1,y2)ax1.text(-11,10,'Original')ax2=fig.add_subplot(122,aspect='equal')ax2.scatter(dbc1[:,0],dbc1[:,1],lw=0.5,color='#00CC00')ax2.scatter(dbc2[:,0],dbc2[:,1],lw=0.5,color='#028E9B')ax2.scatter(noise[:,0],noise[:,1],lw=0.5,color='#FF7800')ax2.xaxis.set_visible(False)ax2.yaxis.set_visible(False)ax2.set_xlim(x1,x2)ax2.set_ylim(y1,y2)ax2.text(-11,10,'DBSCAN identified')fig.savefig('scikits_422_ex1.pdf',bbox_inches='tight')
Nearly all the data points originally defined to be part of the clusters are retained,
and the noisy background data points are excluded (see Figure 4-5). This highlights the advantage of
DBSCAN over kmeans
when data that should not be part of a cluster is present in a sample. This obviously is
dependent on the spatial characteristics of the given distributions.
Get SciPy and NumPy now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.