2.2 Thermal Noise
2.2.1 Additive White Gaussian Noise
In communication systems theory and simulations we often introduce an additive noise n(t) for studying the transceiver performances, as shown in Figure 2.2; either we use its PSD (watts/hertz) when analyzing Eb/N0 or its power (watts) when studying SNR or EVM. Most of the time this noise is assumed additive, white, and Gaussian noise (AWGN).
Figure 2.2 Additive noise introduced in simulations
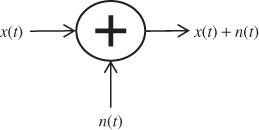
Why this assumption? In practice the AFE of any real communication system is affected by random fluctuations of the charges (electrons) present in any physical device. These fluctuations are known as thermal noise and are dependent on the temperature, as shown next (Davenport and William, 1958; Ott, 1976). For example, in Figure 2.3 a simple passive resistor R generates an RMS noise voltage equal to
where the angle brackets denote the average operator, k = 1.38 × 10−23 J/K is Boltzmann's constant, T is the temperature in kelvin, R is the value of the resistor in ohms, and B is the integration/measurement bandwidth in hertz.
Figure 2.3 Noise voltage generated by a passive resistor

For example, a 50 Ω resistor and 20 MHz bandwidth will ...
Get RF Analog Impairments Modeling for Communication Systems Simulation: Application to OFDM-based Transceivers now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

