Chapter 4. NumPy Basics: Arrays and Vectorized Computation
NumPy, short for Numerical Python, is one of the most important foundational packages for numerical computing in Python. Most computational packages providing scientific functionality use NumPy’s array objects as the lingua franca for data exchange.
Here are some of the things you’ll find in NumPy:
ndarray, an efficient multidimensional array providing fast array-oriented arithmetic operations and flexible broadcasting capabilities.
Mathematical functions for fast operations on entire arrays of data without having to write loops.
Tools for reading/writing array data to disk and working with memory-mapped files.
Linear algebra, random number generation, and Fourier transform capabilities.
A C API for connecting NumPy with libraries written in C, C++, or FORTRAN.
Because NumPy provides an easy-to-use C API, it is straightforward to pass data to external libraries written in a low-level language and also for external libraries to return data to Python as NumPy arrays. This feature has made Python a language of choice for wrapping legacy C/C++/Fortran codebases and giving them a dynamic and easy-to-use interface.
While NumPy by itself does not provide modeling or scientific functionality, having an understanding of NumPy arrays and array-oriented computing will help you use tools with array-oriented semantics, like pandas, much more effectively. Since NumPy is a large topic, I will cover many advanced NumPy features like broadcasting in more depth later (see Appendix A).
For most data analysis applications, the main areas of functionality I’ll focus on are:
Fast vectorized array operations for data munging and cleaning, subsetting and filtering, transformation, and any other kinds of computations
Common array algorithms like sorting, unique, and set operations
Efficient descriptive statistics and aggregating/summarizing data
Data alignment and relational data manipulations for merging and joining together heterogeneous datasets
Expressing conditional logic as array expressions instead of loops with
if-elif-elsebranchesGroup-wise data manipulations (aggregation, transformation, function application)
While NumPy provides a computational foundation for general numerical data processing, many readers will want to use pandas as the basis for most kinds of statistics or analytics, especially on tabular data. pandas also provides some more domain-specific functionality like time series manipulation, which is not present in NumPy.
Note
Array-oriented computing in Python traces its roots back to 1995, when Jim Hugunin created the Numeric library. Over the next 10 years, many scientific programming communities began doing array programming in Python, but the library ecosystem had become fragmented in the early 2000s. In 2005, Travis Oliphant was able to forge the NumPy project from the then Numeric and Numarray projects to bring the community together around a single array computing framework.
One of the reasons NumPy is so important for numerical computations in Python is because it is designed for efficiency on large arrays of data. There are a number of reasons for this:
NumPy internally stores data in a contiguous block of memory, independent of other built-in Python objects. NumPy’s library of algorithms written in the C language can operate on this memory without any type checking or other overhead. NumPy arrays also use much less memory than built-in Python sequences.
NumPy operations perform complex computations on entire arrays without the need for Python
forloops.
To give you an idea of the performance difference, consider a NumPy array of one million integers, and the equivalent Python list:
In[7]:importnumpyasnpIn[8]:my_arr=np.arange(1000000)In[9]:my_list=list(range(1000000))
Now let’s multiply each sequence by 2:
In[10]:%timefor_inrange(10):my_arr2=my_arr*2CPUtimes:user20ms,sys:8ms,total:28msWalltime:26.5msIn[11]:%timefor_inrange(10):my_list2=[x*2forxinmy_list]CPUtimes:user408ms,sys:64ms,total:472msWalltime:473ms
NumPy-based algorithms are generally 10 to 100 times faster (or more) than their pure Python counterparts and use significantly less memory.
4.1 The NumPy ndarray: A Multidimensional Array Object
One of the key features of NumPy is its N-dimensional array object, or ndarray, which is a fast, flexible container for large datasets in Python. Arrays enable you to perform mathematical operations on whole blocks of data using similar syntax to the equivalent operations between scalar elements.
To give you a flavor of how NumPy enables batch computations with similar syntax to scalar values on built-in Python objects, I first import NumPy and generate a small array of random data:
In[12]:importnumpyasnp# Generate some random dataIn[13]:data=np.random.randn(2,3)In[14]:dataOut[14]:array([[-0.2047,0.4789,-0.5194],[-0.5557,1.9658,1.3934]])
I then write mathematical operations with
data:
In[15]:data*10Out[15]:array([[-2.0471,4.7894,-5.1944],[-5.5573,19.6578,13.9341]])In[16]:data+dataOut[16]:array([[-0.4094,0.9579,-1.0389],[-1.1115,3.9316,2.7868]])
In the first example, all of the elements have been multiplied by 10. In the second, the corresponding values in each “cell” in the array have been added to each other.
Note
In this chapter and throughout the book, I use the standard NumPy convention of always using import numpy as np. You are, of course,
welcome to put from numpy import * in
your code to avoid having to write np., but I advise against making a habit of
this. The numpy namespace is large and contains a number of functions whose names
conflict with built-in Python functions (like min and
max).
An ndarray is a generic multidimensional container for homogeneous
data; that is, all of the elements must be the same type. Every array has
a shape, a tuple indicating the size of each dimension, and a dtype, an object describing the data
type of the array:
In[17]:data.shapeOut[17]:(2,3)In[18]:data.dtypeOut[18]:dtype('float64')
This chapter will introduce you to the basics of using NumPy arrays, and should be sufficient for following along with the rest of the book. While it’s not necessary to have a deep understanding of NumPy for many data analytical applications, becoming proficient in array-oriented programming and thinking is a key step along the way to becoming a scientific Python guru.
Note
Whenever you see “array,” “NumPy array,” or “ndarray” in the text, with few exceptions they all refer to the same thing: the ndarray object.
Creating ndarrays
The easiest way to create an array is to use the array function.
This accepts any sequence-like object (including other arrays) and
produces a new NumPy array containing the passed data. For example, a
list is a good candidate for conversion:
In[19]:data1=[6,7.5,8,0,1]In[20]:arr1=np.array(data1)In[21]:arr1Out[21]:array([6.,7.5,8.,0.,1.])
Nested sequences, like a list of equal-length lists, will be converted into a multidimensional array:
In[22]:data2=[[1,2,3,4],[5,6,7,8]]In[23]:arr2=np.array(data2)In[24]:arr2Out[24]:array([[1,2,3,4],[5,6,7,8]])
Since data2 was a list of lists, the NumPy
array arr2 has two dimensions with shape inferred
from the data. We can confirm this by inspecting the ndim and
shape attributes:
In[25]:arr2.ndimOut[25]:2In[26]:arr2.shapeOut[26]:(2,4)
Unless explicitly specified (more on this later), np.array tries to infer a good data type for
the array that it creates. The data type is stored in a special dtype metadata object; for example, in the
previous two examples we have:
In[27]:arr1.dtypeOut[27]:dtype('float64')In[28]:arr2.dtypeOut[28]:dtype('int64')
In addition to np.array, there
are a number of other functions for creating new arrays. As examples,
zeros and ones create arrays of 0s or 1s, respectively, with a given length or shape. empty creates an array without initializing its values to any particular
value. To create a higher dimensional array with these methods, pass a
tuple for the shape:
In[29]:np.zeros(10)Out[29]:array([0.,0.,0.,0.,0.,0.,0.,0.,0.,0.])In[30]:np.zeros((3,6))Out[30]:array([[0.,0.,0.,0.,0.,0.],[0.,0.,0.,0.,0.,0.],[0.,0.,0.,0.,0.,0.]])In[31]:np.empty((2,3,2))Out[31]:array([[[0.,0.],[0.,0.],[0.,0.]],[[0.,0.],[0.,0.],[0.,0.]]])
Caution
It’s not safe to assume that np.empty will return an array of all zeros.
In some cases, it may return uninitialized “garbage” values.
arange is an array-valued
version of the built-in Python range
function:
In[32]:np.arange(15)Out[32]:array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14])
See Table 4-1 for a short list of
standard array creation functions. Since NumPy is focused on numerical
computing, the data type, if not specified, will in many cases be
float64 (floating point).
Data Types for ndarrays
The data type or dtype is a special object containing the information (or
metadata, data about data) the ndarray needs to
interpret a chunk of memory as a particular type of data:
In[33]:arr1=np.array([1,2,3],dtype=np.float64)In[34]:arr2=np.array([1,2,3],dtype=np.int32)In[35]:arr1.dtypeOut[35]:dtype('float64')In[36]:arr2.dtypeOut[36]:dtype('int32')
dtypes are a source of NumPy’s flexibility for interacting with
data coming from other systems. In most cases they provide a mapping
directly onto an underlying disk or memory representation, which makes
it easy to read and write binary streams of data to disk and also to
connect to code written in a low-level language like C or Fortran. The
numerical dtypes are named the same way: a type name, like float or int, followed by a number indicating the
number of bits per element. A standard double-precision floating-point
value (what’s used under the hood in Python’s float object) takes up 8 bytes or 64 bits.
Thus, this type is known in NumPy as float64. See Table 4-2 for a full listing of NumPy’s supported
data types.
Note
Don’t worry about memorizing the NumPy dtypes, especially if you’re a new user. It’s often only necessary to care about the general kind of data you’re dealing with, whether floating point, complex, integer, boolean, string, or general Python object. When you need more control over how data are stored in memory and on disk, especially large datasets, it is good to know that you have control over the storage type.
You can explicitly convert or cast an array
from one dtype to another using ndarray’s astype
method:
In[37]:arr=np.array([1,2,3,4,5])In[38]:arr.dtypeOut[38]:dtype('int64')In[39]:float_arr=arr.astype(np.float64)In[40]:float_arr.dtypeOut[40]:dtype('float64')
In this example, integers were cast to floating point. If I cast some floating-point numbers to be of integer dtype, the decimal part will be truncated:
In[41]:arr=np.array([3.7,-1.2,-2.6,0.5,12.9,10.1])In[42]:arrOut[42]:array([3.7,-1.2,-2.6,0.5,12.9,10.1])In[43]:arr.astype(np.int32)Out[43]:array([3,-1,-2,0,12,10],dtype=int32)
If you have an array of strings representing numbers, you can use
astype to convert them to numeric
form:
In[44]:numeric_strings=np.array(['1.25','-9.6','42'],dtype=np.string_)In[45]:numeric_strings.astype(float)Out[45]:array([1.25,-9.6,42.])
Caution
It’s important to be cautious when using the
numpy.string_ type, as string data in NumPy is
fixed size and may truncate input without warning. pandas has more
intuitive out-of-the-box behavior on non-numeric data.
If casting were to fail for some reason (like a string that cannot
be converted to float64), a
ValueError will be raised. Here I was
a bit lazy and wrote float instead of
np.float64; NumPy aliases the Python
types to its own equivalent data dtypes.
You can also use another array’s dtype attribute:
In[46]:int_array=np.arange(10)In[47]:calibers=np.array([.22,.270,.357,.380,.44,.50],dtype=np.float64)In[48]:int_array.astype(calibers.dtype)Out[48]:array([0.,1.,2.,3.,4.,5.,6.,7.,8.,9.])
There are shorthand type code strings you can also use to refer to a dtype:
In[49]:empty_uint32=np.empty(8,dtype='u4')In[50]:empty_uint32Out[50]:array([0,1075314688,0,1075707904,0,1075838976,0,1072693248],dtype=uint32)
Note
Calling astype
always creates a new array (a copy of the data),
even if the new dtype is the same as the old dtype.
Arithmetic with NumPy Arrays
Arrays are important because they enable you to express batch operations on
data without writing any for loops.
NumPy users call this vectorization. Any arithmetic
operations between equal-size arrays applies the operation
element-wise:
In[51]:arr=np.array([[1.,2.,3.],[4.,5.,6.]])In[52]:arrOut[52]:array([[1.,2.,3.],[4.,5.,6.]])In[53]:arr*arrOut[53]:array([[1.,4.,9.],[16.,25.,36.]])In[54]:arr-arrOut[54]:array([[0.,0.,0.],[0.,0.,0.]])
Arithmetic operations with scalars propagate the scalar argument to each element in the array:
In[55]:1/arrOut[55]:array([[1.,0.5,0.3333],[0.25,0.2,0.1667]])In[56]:arr**0.5Out[56]:array([[1.,1.4142,1.7321],[2.,2.2361,2.4495]])
Comparisons between arrays of the same size yield boolean arrays:
In[57]:arr2=np.array([[0.,4.,1.],[7.,2.,12.]])In[58]:arr2Out[58]:array([[0.,4.,1.],[7.,2.,12.]])In[59]:arr2>arrOut[59]:array([[False,True,False],[True,False,True]])
Evaluating operations between differently sized arrays is called broadcasting and will be discussed in more detail in Appendix A. Having a deep understanding of broadcasting is not necessary for most of this book.
Basic Indexing and Slicing
NumPy array indexing is a rich topic, as there are many ways you may want to select a subset of your data or individual elements. One-dimensional arrays are simple; on the surface they act similarly to Python lists:
In[60]:arr=np.arange(10)In[61]:arrOut[61]:array([0,1,2,3,4,5,6,7,8,9])In[62]:arr[5]Out[62]:5In[63]:arr[5:8]Out[63]:array([5,6,7])In[64]:arr[5:8]=12In[65]:arrOut[65]:array([0,1,2,3,4,12,12,12,8,9])
As you can see, if you assign a scalar value to a slice, as in
arr[5:8] = 12, the value is
propagated (or broadcasted henceforth) to the
entire selection. An important first distinction from Python’s built-in
lists is that array slices are views on the
original array. This means that the data is not copied, and any
modifications to the view will be reflected in the source array.
To give an example of this, I first create a slice of
arr:
In[66]:arr_slice=arr[5:8]In[67]:arr_sliceOut[67]:array([12,12,12])
Now, when I change values in arr_slice, the
mutations are reflected in the original array
arr:
In[68]:arr_slice[1]=12345In[69]:arrOut[69]:array([0,1,2,3,4,12,12345,12,8,9])
The “bare” slice [:] will assign to all values
in an array:
In[70]:arr_slice[:]=64In[71]:arrOut[71]:array([0,1,2,3,4,64,64,64,8,9])
If you are new to NumPy, you might be surprised by this, especially if you have used other array programming languages that copy data more eagerly. As NumPy has been designed to be able to work with very large arrays, you could imagine performance and memory problems if NumPy insisted on always copying data.
Caution
If you want a copy of a slice of an ndarray instead of a view,
you will need to explicitly copy the array—for example, arr[5:8].copy().
With higher dimensional arrays, you have many more options. In a two-dimensional array, the elements at each index are no longer scalars but rather one-dimensional arrays:
In[72]:arr2d=np.array([[1,2,3],[4,5,6],[7,8,9]])In[73]:arr2d[2]Out[73]:array([7,8,9])
Thus, individual elements can be accessed recursively. But that is a bit too much work, so you can pass a comma-separated list of indices to select individual elements. So these are equivalent:
In[74]:arr2d[0][2]Out[74]:3In[75]:arr2d[0,2]Out[75]:3
See Figure 4-1 for an illustration of indexing on a two-dimensional array. I find it helpful to think of axis 0 as the “rows” of the array and axis 1 as the “columns.”
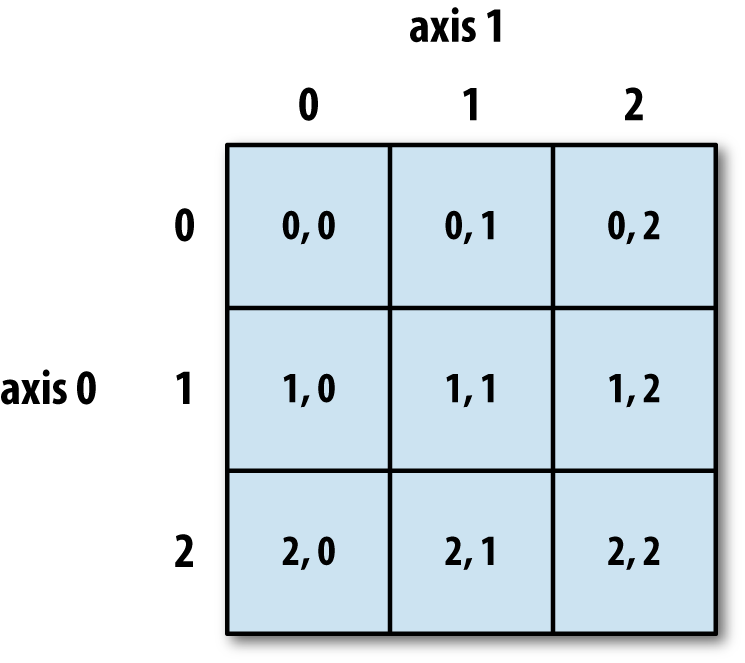
Figure 4-1. Indexing elements in a NumPy array
In multidimensional arrays, if you omit later indices, the
returned object will be a lower dimensional ndarray consisting of all
the data along the higher dimensions. So in the 2 × 2 × 3 array arr3d:
In[76]:arr3d=np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])In[77]:arr3dOut[77]:array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
arr3d[0] is a 2 × 3
array:
In[78]:arr3d[0]Out[78]:array([[1,2,3],[4,5,6]])
Both scalar values and arrays can be assigned to arr3d[0]:
In[79]:old_values=arr3d[0].copy()In[80]:arr3d[0]=42In[81]:arr3dOut[81]:array([[[42,42,42],[42,42,42]],[[7,8,9],[10,11,12]]])In[82]:arr3d[0]=old_valuesIn[83]:arr3dOut[83]:array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
Similarly, arr3d[1, 0] gives
you all of the values whose indices start with (1, 0), forming a 1-dimensional array:
In[84]:arr3d[1,0]Out[84]:array([7,8,9])
This expression is the same as though we had indexed in two steps:
In[85]:x=arr3d[1]In[86]:xOut[86]:array([[7,8,9],[10,11,12]])In[87]:x[0]Out[87]:array([7,8,9])
Note that in all of these cases where subsections of the array have been selected, the returned arrays are views.
Indexing with slices
Like one-dimensional objects such as Python lists, ndarrays can be sliced with the familiar syntax:
In[88]:arrOut[88]:array([0,1,2,3,4,64,64,64,8,9])In[89]:arr[1:6]Out[89]:array([1,2,3,4,64])
Consider the two-dimensional array from before, arr2d. Slicing this array is a bit
different:
In[90]:arr2dOut[90]:array([[1,2,3],[4,5,6],[7,8,9]])In[91]:arr2d[:2]Out[91]:array([[1,2,3],[4,5,6]])
As you can see, it has sliced along axis 0, the first axis. A
slice, therefore, selects a range of elements along an axis. It can be
helpful to read the expression arr2d[:2] as “select
the first two rows of arr2d.”
You can pass multiple slices just like you can pass multiple indexes:
In[92]:arr2d[:2,1:]Out[92]:array([[2,3],[5,6]])
When slicing like this, you always obtain array views of the same number of dimensions. By mixing integer indexes and slices, you get lower dimensional slices.
For example, I can select the second row but only the first two columns like so:
In[93]:arr2d[1,:2]Out[93]:array([4,5])
Similarly, I can select the third column but only the first two rows like so:
In[94]:arr2d[:2,2]Out[94]:array([3,6])
See Figure 4-2 for an illustration. Note that a colon by itself means to take the entire axis, so you can slice only higher dimensional axes by doing:
In[95]:arr2d[:,:1]Out[95]:array([[1],[4],[7]])
Of course, assigning to a slice expression assigns to the whole selection:
In[96]:arr2d[:2,1:]=0In[97]:arr2dOut[97]:array([[1,0,0],[4,0,0],[7,8,9]])
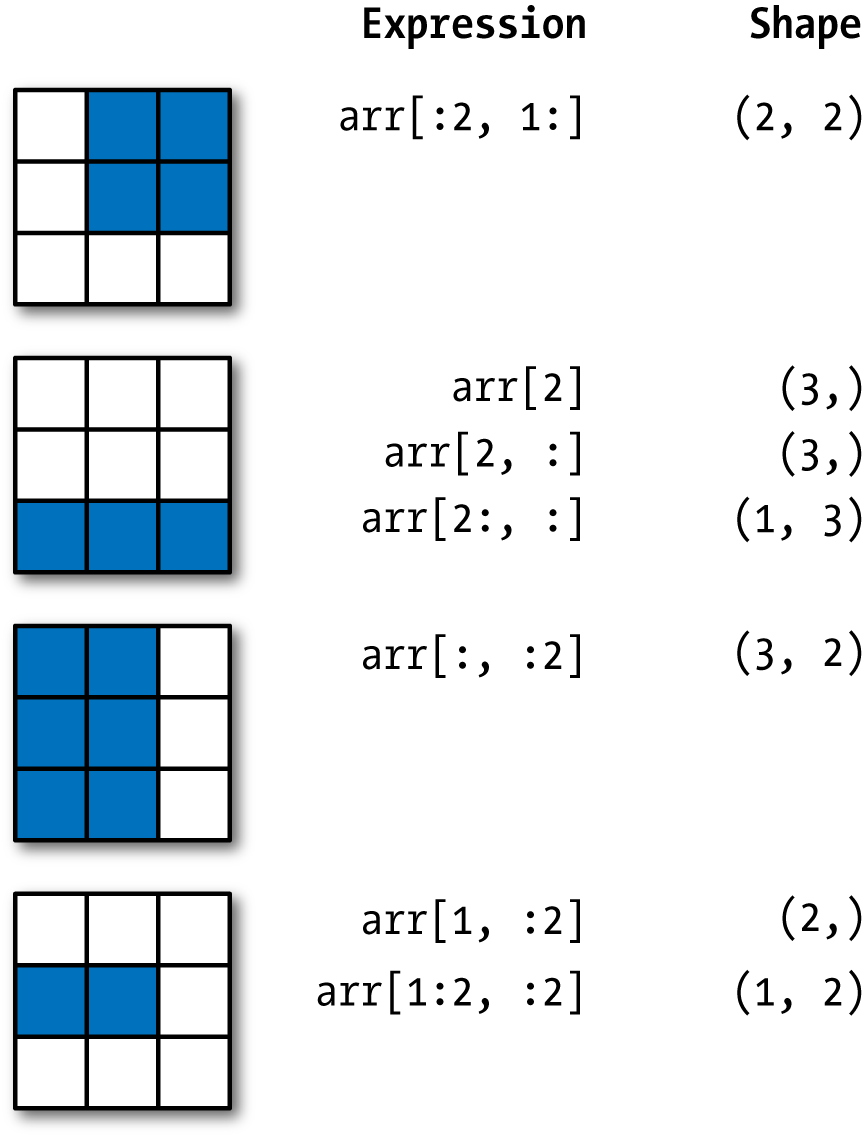
Figure 4-2. Two-dimensional array slicing
Boolean Indexing
Let’s consider an example where we have some data in an array
and an array of names with duplicates. I’m going to use here the randn function in
numpy.random to generate some random
normally distributed data:
In[98]:names=np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])In[99]:data=np.random.randn(7,4)In[100]:namesOut[100]:array(['Bob','Joe','Will','Bob','Will','Joe','Joe'],dtype='<U4')In[101]:dataOut[101]:array([[0.0929,0.2817,0.769,1.2464],[1.0072,-1.2962,0.275,0.2289],[1.3529,0.8864,-2.0016,-0.3718],[1.669,-0.4386,-0.5397,0.477],[3.2489,-1.0212,-0.5771,0.1241],[0.3026,0.5238,0.0009,1.3438],[-0.7135,-0.8312,-2.3702,-1.8608]])
Suppose each name corresponds to a row in the data array and we wanted to select all the
rows with corresponding name 'Bob'.
Like arithmetic operations, comparisons (such as ==) with arrays are also vectorized. Thus,
comparing names with
the string 'Bob' yields a boolean
array:
In[102]:names=='Bob'Out[102]:array([True,False,False,True,False,False,False])
This boolean array can be passed when indexing the array:
In[103]:data[names=='Bob']Out[103]:array([[0.0929,0.2817,0.769,1.2464],[1.669,-0.4386,-0.5397,0.477]])
The boolean array must be of the same length as the array axis it’s indexing. You can even mix and match boolean arrays with slices or integers (or sequences of integers; more on this later).
In these examples, I select from the rows where names ==
'Bob' and index the columns, too:
In[104]:data[names=='Bob',2:]Out[104]:array([[0.769,1.2464],[-0.5397,0.477]])In[105]:data[names=='Bob',3]Out[105]:array([1.2464,0.477])
To select everything but 'Bob',
you can either use != or negate the
condition using ~:
In[106]:names!='Bob'Out[106]:array([False,True,True,False,True,True,True])In[107]:data[~(names=='Bob')]Out[107]:array([[1.0072,-1.2962,0.275,0.2289],[1.3529,0.8864,-2.0016,-0.3718],[3.2489,-1.0212,-0.5771,0.1241],[0.3026,0.5238,0.0009,1.3438],[-0.7135,-0.8312,-2.3702,-1.8608]])
The ~ operator can be useful when you want to invert a general
condition:
In[108]:cond=names=='Bob'In[109]:data[~cond]Out[109]:array([[1.0072,-1.2962,0.275,0.2289],[1.3529,0.8864,-2.0016,-0.3718],[3.2489,-1.0212,-0.5771,0.1241],[0.3026,0.5238,0.0009,1.3438],[-0.7135,-0.8312,-2.3702,-1.8608]])
Selecting two of the three names to combine multiple boolean
conditions, use boolean arithmetic operators like & (and) and | (or):
In[110]:mask=(names=='Bob')|(names=='Will')In[111]:maskOut[111]:array([True,False,True,True,True,False,False])In[112]:data[mask]Out[112]:array([[0.0929,0.2817,0.769,1.2464],[1.3529,0.8864,-2.0016,-0.3718],[1.669,-0.4386,-0.5397,0.477],[3.2489,-1.0212,-0.5771,0.1241]])
Selecting data from an array by boolean indexing always creates a copy of the data, even if the returned array is unchanged.
Caution
The Python keywords and and
or do not work with boolean arrays. Use
& (and) and | (or)
instead.
Setting values with boolean arrays works in a common-sense way. To
set all of the negative values in data to 0 we need only do:
In[113]:data[data<0]=0In[114]:dataOut[114]:array([[0.0929,0.2817,0.769,1.2464],[1.0072,0.,0.275,0.2289],[1.3529,0.8864,0.,0.],[1.669,0.,0.,0.477],[3.2489,0.,0.,0.1241],[0.3026,0.5238,0.0009,1.3438],[0.,0.,0.,0.]])
Setting whole rows or columns using a one-dimensional boolean array is also easy:
In[115]:data[names!='Joe']=7In[116]:dataOut[116]:array([[7.,7.,7.,7.],[1.0072,0.,0.275,0.2289],[7.,7.,7.,7.],[7.,7.,7.,7.],[7.,7.,7.,7.],[0.3026,0.5238,0.0009,1.3438],[0.,0.,0.,0.]])
As we will see later, these types of operations on two-dimensional data are convenient to do with pandas.
Fancy Indexing
Fancy indexing is a term adopted by NumPy to describe indexing using integer arrays. Suppose we had an 8 × 4 array:
In[117]:arr=np.empty((8,4))In[118]:foriinrange(8):.....:arr[i]=iIn[119]:arrOut[119]:array([[0.,0.,0.,0.],[1.,1.,1.,1.],[2.,2.,2.,2.],[3.,3.,3.,3.],[4.,4.,4.,4.],[5.,5.,5.,5.],[6.,6.,6.,6.],[7.,7.,7.,7.]])
To select out a subset of the rows in a particular order, you can simply pass a list or ndarray of integers specifying the desired order:
In[120]:arr[[4,3,0,6]]Out[120]:array([[4.,4.,4.,4.],[3.,3.,3.,3.],[0.,0.,0.,0.],[6.,6.,6.,6.]])
Hopefully this code did what you expected! Using negative indices selects rows from the end:
In[121]:arr[[-3,-5,-7]]Out[121]:array([[5.,5.,5.,5.],[3.,3.,3.,3.],[1.,1.,1.,1.]])
Passing multiple index arrays does something slightly different; it selects a one-dimensional array of elements corresponding to each tuple of indices:
In[122]:arr=np.arange(32).reshape((8,4))In[123]:arrOut[123]:array([[0,1,2,3],[4,5,6,7],[8,9,10,11],[12,13,14,15],[16,17,18,19],[20,21,22,23],[24,25,26,27],[28,29,30,31]])In[124]:arr[[1,5,7,2],[0,3,1,2]]Out[124]:array([4,23,29,10])
We’ll look at the reshape method in more detail in
Appendix A.
Here the elements (1, 0), (5, 3), (7,
1), and (2, 2) were
selected. Regardless of how many dimensions the array has (here, only 2),
the result of fancy indexing with multiple integer arrays is always
one-dimensional.
The behavior of fancy indexing in this case is a bit different from what some users might have expected (myself included), which is the rectangular region formed by selecting a subset of the matrix’s rows and columns. Here is one way to get that:
In[125]:arr[[1,5,7,2]][:,[0,3,1,2]]Out[125]:array([[4,7,5,6],[20,23,21,22],[28,31,29,30],[8,11,9,10]])
Keep in mind that fancy indexing, unlike slicing, always copies the data into a new array.
Transposing Arrays and Swapping Axes
Transposing is a special form of reshaping that similarly returns a view
on the underlying data without copying anything. Arrays have the transpose method
and also the special T
attribute:
In[126]:arr=np.arange(15).reshape((3,5))In[127]:arrOut[127]:array([[0,1,2,3,4],[5,6,7,8,9],[10,11,12,13,14]])In[128]:arr.TOut[128]:array([[0,5,10],[1,6,11],[2,7,12],[3,8,13],[4,9,14]])
When doing matrix computations, you may do this very often—for
example, when computing the inner matrix product using np.dot:
In[129]:arr=np.random.randn(6,3)In[130]:arrOut[130]:array([[-0.8608,0.5601,-1.2659],[0.1198,-1.0635,0.3329],[-2.3594,-0.1995,-1.542],[-0.9707,-1.307,0.2863],[0.378,-0.7539,0.3313],[1.3497,0.0699,0.2467]])In[131]:np.dot(arr.T,arr)Out[131]:array([[9.2291,0.9394,4.948],[0.9394,3.7662,-1.3622],[4.948,-1.3622,4.3437]])
For higher dimensional arrays, transpose will accept a tuple of axis numbers
to permute the axes (for extra mind bending):
In[132]:arr=np.arange(16).reshape((2,2,4))In[133]:arrOut[133]:array([[[0,1,2,3],[4,5,6,7]],[[8,9,10,11],[12,13,14,15]]])In[134]:arr.transpose((1,0,2))Out[134]:array([[[0,1,2,3],[8,9,10,11]],[[4,5,6,7],[12,13,14,15]]])
Here, the axes have been reordered with the second axis first, the first axis second, and the last axis unchanged.
Simple transposing with .T is a
special case of swapping axes. ndarray has the method swapaxes, which
takes a pair of axis numbers and switches the indicated axes to
rearrange the data:
In[135]:arrOut[135]:array([[[0,1,2,3],[4,5,6,7]],[[8,9,10,11],[12,13,14,15]]])In[136]:arr.swapaxes(1,2)Out[136]:array([[[0,4],[1,5],[2,6],[3,7]],[[8,12],[9,13],[10,14],[11,15]]])
swapaxes similarly returns a
view on the data without making a copy.
4.2 Universal Functions: Fast Element-Wise Array Functions
A universal function, or ufunc, is a function that performs element-wise operations on data in ndarrays. You can think of them as fast vectorized wrappers for simple functions that take one or more scalar values and produce one or more scalar results.
Many ufuncs are simple element-wise transformations, like sqrt or exp:
In[137]:arr=np.arange(10)In[138]:arrOut[138]:array([0,1,2,3,4,5,6,7,8,9])In[139]:np.sqrt(arr)Out[139]:array([0.,1.,1.4142,1.7321,2.,2.2361,2.4495,2.6458,2.8284,3.])In[140]:np.exp(arr)Out[140]:array([1.,2.7183,7.3891,20.0855,54.5982,148.4132,403.4288,1096.6332,2980.958,8103.0839])
These are referred to as unary ufuncs. Others, such as
add or maximum, take two arrays (thus,
binary ufuncs) and return a single array as the result:
In[141]:x=np.random.randn(8)In[142]:y=np.random.randn(8)In[143]:xOut[143]:array([-0.0119,1.0048,1.3272,-0.9193,-1.5491,0.0222,0.7584,-0.6605])In[144]:yOut[144]:array([0.8626,-0.01,0.05,0.6702,0.853,-0.9559,-0.0235,-2.3042])In[145]:np.maximum(x,y)Out[145]:array([0.8626,1.0048,1.3272,0.6702,0.853,0.0222,0.7584,-0.6605])
Here, numpy.maximum computed the element-wise
maximum of the elements in x and
y.
While not common, a ufunc can return multiple arrays. modf is one example, a vectorized version of the built-in Python
divmod; it returns the fractional and integral parts of a
floating-point array:
In[146]:arr=np.random.randn(7)*5In[147]:arrOut[147]:array([-3.2623,-6.0915,-6.663,5.3731,3.6182,3.45,5.0077])In[148]:remainder,whole_part=np.modf(arr)In[149]:remainderOut[149]:array([-0.2623,-0.0915,-0.663,0.3731,0.6182,0.45,0.0077])In[150]:whole_partOut[150]:array([-3.,-6.,-6.,5.,3.,3.,5.])
Ufuncs accept an optional out argument that
allows them to operate in-place on arrays:
In[151]:arrOut[151]:array([-3.2623,-6.0915,-6.663,5.3731,3.6182,3.45,5.0077])In[152]:np.sqrt(arr)Out[152]:array([nan,nan,nan,2.318,1.9022,1.8574,2.2378])In[153]:np.sqrt(arr,arr)Out[153]:array([nan,nan,nan,2.318,1.9022,1.8574,2.2378])In[154]:arrOut[154]:array([nan,nan,nan,2.318,1.9022,1.8574,2.2378])
See Tables 4-3 and 4-4 for a listing of available ufuncs.
4.3 Array-Oriented Programming with Arrays
Using NumPy arrays enables you to express many kinds of data processing tasks as concise array expressions that might otherwise require writing loops. This practice of replacing explicit loops with array expressions is commonly referred to as vectorization. In general, vectorized array operations will often be one or two (or more) orders of magnitude faster than their pure Python equivalents, with the biggest impact in any kind of numerical computations. Later, in Appendix A, I explain broadcasting, a powerful method for vectorizing computations.
As a simple example, suppose we wished to evaluate the function
sqrt(x^2 + y^2) across a regular grid
of values. The np.meshgrid function
takes two 1D arrays and produces two 2D matrices
corresponding to all pairs of (x, y) in
the two arrays:
In[155]:points=np.arange(-5,5,0.01)# 1000 equally spaced pointsIn[156]:xs,ys=np.meshgrid(points,points)In[157]:ysOut[157]:array([[-5.,-5.,-5.,...,-5.,-5.,-5.],[-4.99,-4.99,-4.99,...,-4.99,-4.99,-4.99],[-4.98,-4.98,-4.98,...,-4.98,-4.98,-4.98],...,[4.97,4.97,4.97,...,4.97,4.97,4.97],[4.98,4.98,4.98,...,4.98,4.98,4.98],[4.99,4.99,4.99,...,4.99,4.99,4.99]])
Now, evaluating the function is a matter of writing the same expression you would write with two points:
In[158]:z=np.sqrt(xs**2+ys**2)In[159]:zOut[159]:array([[7.0711,7.064,7.0569,...,7.0499,7.0569,7.064],[7.064,7.0569,7.0499,...,7.0428,7.0499,7.0569],[7.0569,7.0499,7.0428,...,7.0357,7.0428,7.0499],...,[7.0499,7.0428,7.0357,...,7.0286,7.0357,7.0428],[7.0569,7.0499,7.0428,...,7.0357,7.0428,7.0499],[7.064,7.0569,7.0499,...,7.0428,7.0499,7.0569]])
As a preview of Chapter 9, I use matplotlib to create visualizations of this two-dimensional array:
In[160]:importmatplotlib.pyplotaspltIn[161]:plt.imshow(z,cmap=plt.cm.gray);plt.colorbar()Out[161]:<matplotlib.colorbar.Colorbarat0x7f8520cd1b38>In[162]:plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")Out[162]:Text(0.5,1,'Image plot of $\\sqrt{x^2 + y^2}$ for a grid of values')
See Figure 4-3. Here I used the
matplotlib function imshow to
create an image plot from a two-dimensional array of
function values.

Figure 4-3. Plot of function evaluated on grid
Expressing Conditional Logic as Array Operations
The numpy.where function is a
vectorized version of the ternary expression x if condition else y. Suppose we had a
boolean array and two arrays of values:
In[165]:xarr=np.array([1.1,1.2,1.3,1.4,1.5])In[166]:yarr=np.array([2.1,2.2,2.3,2.4,2.5])In[167]:cond=np.array([True,False,True,True,False])
Suppose we wanted to take a value from xarr whenever the corresponding value in
cond is True, and otherwise take the value from yarr. A list comprehension doing this might
look like:
In[168]:result=[(xifcelsey).....:forx,y,cinzip(xarr,yarr,cond)]In[169]:resultOut[169]:[1.1,2.2,1.3,1.4,2.5]
This has multiple problems. First, it will not be very fast for
large arrays (because all the work is being done in interpreted Python
code). Second, it will not work with multidimensional arrays. With
np.where you can write this very
concisely:
In[170]:result=np.where(cond,xarr,yarr)In[171]:resultOut[171]:array([1.1,2.2,1.3,1.4,2.5])
The second and third arguments to np.where don’t need to be arrays; one or both
of them can be scalars. A typical use of where in data analysis is to produce a new
array of values based on another array. Suppose you had a matrix of
randomly generated data and you wanted to replace all positive values
with 2 and all negative values with –2. This is very easy to do with
np.where:
In[172]:arr=np.random.randn(4,4)In[173]:arrOut[173]:array([[-0.5031,-0.6223,-0.9212,-0.7262],[0.2229,0.0513,-1.1577,0.8167],[0.4336,1.0107,1.8249,-0.9975],[0.8506,-0.1316,0.9124,0.1882]])In[174]:arr>0Out[174]:array([[False,False,False,False],[True,True,False,True],[True,True,True,False],[True,False,True,True]])In[175]:np.where(arr>0,2,-2)Out[175]:array([[-2,-2,-2,-2],[2,2,-2,2],[2,2,2,-2],[2,-2,2,2]])
You can combine scalars and arrays when using
np.where. For example, I can replace all positive
values in arr with the constant 2 like so:
In[176]:np.where(arr>0,2,arr)# set only positive values to 2Out[176]:array([[-0.5031,-0.6223,-0.9212,-0.7262],[2.,2.,-1.1577,2.],[2.,2.,2.,-0.9975],[2.,-0.1316,2.,2.]])
The arrays passed to np.where can be more than
just equal-sized arrays or scalars.
Mathematical and Statistical Methods
A set of mathematical functions that compute statistics about an entire array or about
the data along an axis are accessible as methods of the array class.
You can use aggregations (often called reductions) like sum, mean,
and std (standard deviation) either
by calling the array instance method or using the top-level
NumPy function.
Here I generate some normally distributed random data and compute some aggregate statistics:
In[177]:arr=np.random.randn(5,4)In[178]:arrOut[178]:array([[2.1695,-0.1149,2.0037,0.0296],[0.7953,0.1181,-0.7485,0.585],[0.1527,-1.5657,-0.5625,-0.0327],[-0.929,-0.4826,-0.0363,1.0954],[0.9809,-0.5895,1.5817,-0.5287]])In[179]:arr.mean()Out[179]:0.19607051119998253In[180]:np.mean(arr)Out[180]:0.19607051119998253In[181]:arr.sum()Out[181]:3.9214102239996507
Functions like mean and
sum take an optional axis argument that computes the statistic
over the given axis, resulting in an array with one fewer
dimension:
In[182]:arr.mean(axis=1)Out[182]:array([1.022,0.1875,-0.502,-0.0881,0.3611])In[183]:arr.sum(axis=0)Out[183]:array([3.1693,-2.6345,2.2381,1.1486])
Here, arr.mean(1) means “compute mean across the columns” where
arr.sum(0) means “compute sum down the rows.”
Other methods like cumsum and
cumprod do not aggregate, instead
producing an array of the intermediate results:
In[184]:arr=np.array([0,1,2,3,4,5,6,7])In[185]:arr.cumsum()Out[185]:array([0,1,3,6,10,15,21,28])
In multidimensional arrays, accumulation functions like
cumsum return an array of the same size, but with the
partial aggregates computed along the indicated axis according to each
lower dimensional slice:
In[186]:arr=np.array([[0,1,2],[3,4,5],[6,7,8]])In[187]:arrOut[187]:array([[0,1,2],[3,4,5],[6,7,8]])In[188]:arr.cumsum(axis=0)Out[188]:array([[0,1,2],[3,5,7],[9,12,15]])In[189]:arr.cumprod(axis=1)Out[189]:array([[0,0,0],[3,12,60],[6,42,336]])
See Table 4-5 for a full listing. We’ll see many examples of these methods in action in later chapters.
Methods for Boolean Arrays
Boolean values are coerced to 1 (True)
and 0 (False) in the preceding
methods. Thus, sum is often used as a
means of counting True values in a
boolean array:
In[190]:arr=np.random.randn(100)In[191]:(arr>0).sum()# Number of positive valuesOut[191]:42
There are two additional methods, any and
all, useful especially for boolean
arrays. any tests whether one or more
values in an array is True, while
all checks if every value is True:
In[192]:bools=np.array([False,False,True,False])In[193]:bools.any()Out[193]:TrueIn[194]:bools.all()Out[194]:False
These methods also work with non-boolean arrays, where non-zero
elements evaluate to True.
Sorting
Like Python’s built-in list type, NumPy arrays can be sorted in-place with the sort method:
In[195]:arr=np.random.randn(6)In[196]:arrOut[196]:array([0.6095,-0.4938,1.24,-0.1357,1.43,-0.8469])In[197]:arr.sort()In[198]:arrOut[198]:array([-0.8469,-0.4938,-0.1357,0.6095,1.24,1.43])
You can sort each one-dimensional section of values in a multidimensional array
in-place along an axis by passing the axis number to
sort:
In[199]:arr=np.random.randn(5,3)In[200]:arrOut[200]:array([[0.6033,1.2636,-0.2555],[-0.4457,0.4684,-0.9616],[-1.8245,0.6254,1.0229],[1.1074,0.0909,-0.3501],[0.218,-0.8948,-1.7415]])In[201]:arr.sort(1)In[202]:arrOut[202]:array([[-0.2555,0.6033,1.2636],[-0.9616,-0.4457,0.4684],[-1.8245,0.6254,1.0229],[-0.3501,0.0909,1.1074],[-1.7415,-0.8948,0.218]])
The top-level method np.sort
returns a sorted copy of an array instead of modifying the array
in-place. A quick-and-dirty way to compute the quantiles of an array is
to sort it and select the value at a particular rank:
In[203]:large_arr=np.random.randn(1000)In[204]:large_arr.sort()In[205]:large_arr[int(0.05*len(large_arr))]# 5% quantileOut[205]:-1.5311513550102103
For more details on using NumPy’s sorting methods, and more advanced techniques like indirect sorts, see Appendix A. Several other kinds of data manipulations related to sorting (e.g., sorting a table of data by one or more columns) can also be found in pandas.
Unique and Other Set Logic
NumPy has some basic set operations for one-dimensional ndarrays. A commonly
used one is np.unique, which
returns the sorted unique values in an array:
In[206]:names=np.array(['Bob','Joe','Will','Bob','Will','Joe','Joe'])In[207]:np.unique(names)Out[207]:array(['Bob','Joe','Will'],dtype='<U4')In[208]:ints=np.array([3,3,3,2,2,1,1,4,4])In[209]:np.unique(ints)Out[209]:array([1,2,3,4])
Contrast np.unique with the
pure Python alternative:
In[210]:sorted(set(names))Out[210]:['Bob','Joe','Will']
Another function, np.in1d,
tests membership of the values in one array in another,
returning a boolean array:
In[211]:values=np.array([6,0,0,3,2,5,6])In[212]:np.in1d(values,[2,3,6])Out[212]:array([True,False,False,True,True,False,True])
See Table 4-6 for a listing of set functions in NumPy.
4.4 File Input and Output with Arrays
NumPy is able to save and load data to and from disk either in text or binary format. In this section I only discuss NumPy’s built-in binary format, since most users will prefer pandas and other tools for loading text or tabular data (see Chapter 6 for much more).
np.save and np.load are the two workhorse functions for efficiently saving and
loading array data on disk. Arrays are saved by default in an uncompressed
raw binary format with file extension .npy:
In[213]:arr=np.arange(10)In[214]:np.save('some_array',arr)
If the file path does not already end in .npy,
the extension will be appended. The array on disk can then be loaded with
np.load:
In[215]:np.load('some_array.npy')Out[215]:array([0,1,2,3,4,5,6,7,8,9])
You save multiple arrays in an uncompressed archive using np.savez and
passing the arrays as keyword arguments:
In[216]:np.savez('array_archive.npz',a=arr,b=arr)
When loading an .npz file, you get back a dict-like object that loads the individual arrays lazily:
In[217]:arch=np.load('array_archive.npz')In[218]:arch['b']Out[218]:array([0,1,2,3,4,5,6,7,8,9])
If your data compresses well, you may wish to use numpy.savez_compressed
instead:
In[219]:np.savez_compressed('arrays_compressed.npz',a=arr,b=arr)
4.5 Linear Algebra
Linear algebra, like matrix multiplication, decompositions, determinants,
and other square matrix math, is an important part of any array library.
Unlike some languages like MATLAB, multiplying two two-dimensional arrays
with * is an element-wise product
instead of a matrix dot product. Thus, there is a function dot, both an array method and a function in the numpy namespace, for matrix multiplication:
In[223]:x=np.array([[1.,2.,3.],[4.,5.,6.]])In[224]:y=np.array([[6.,23.],[-1,7],[8,9]])In[225]:xOut[225]:array([[1.,2.,3.],[4.,5.,6.]])In[226]:yOut[226]:array([[6.,23.],[-1.,7.],[8.,9.]])In[227]:x.dot(y)Out[227]:array([[28.,64.],[67.,181.]])
x.dot(y) is equivalent to np.dot(x,
y):
In[228]:np.dot(x,y)Out[228]:array([[28.,64.],[67.,181.]])
A matrix product between a two-dimensional array and a suitably sized one-dimensional array results in a one-dimensional array:
In[229]:np.dot(x,np.ones(3))Out[229]:array([6.,15.])
The @ symbol (as of Python 3.5) also works as an infix operator that
performs matrix multiplication:
In[230]:x@np.ones(3)Out[230]:array([6.,15.])
numpy.linalg has a standard set
of matrix decompositions and things like inverse and determinant. These
are implemented under the hood via the same industry-standard linear
algebra libraries used in other languages like MATLAB and R, such as BLAS,
LAPACK, or possibly (depending on your NumPy build) the proprietary
Intel MKL (Math Kernel Library):
In[231]:fromnumpy.linalgimportinv,qrIn[232]:X=np.random.randn(5,5)In[233]:mat=X.T.dot(X)In[234]:inv(mat)Out[234]:array([[933.1189,871.8258,-1417.6902,-1460.4005,1782.1391],[871.8258,815.3929,-1325.9965,-1365.9242,1666.9347],[-1417.6902,-1325.9965,2158.4424,2222.0191,-2711.6822],[-1460.4005,-1365.9242,2222.0191,2289.0575,-2793.422],[1782.1391,1666.9347,-2711.6822,-2793.422,3409.5128]])In[235]:mat.dot(inv(mat))Out[235]:array([[1.,0.,0.,0.,0.],[0.,1.,-0.,-0.,-0.],[-0.,-0.,1.,0.,-0.],[0.,0.,0.,1.,0.],[0.,0.,-0.,-0.,1.]])In[236]:q,r=qr(mat)In[237]:rOut[237]:array([[-1.6914,4.38,0.1757,0.4075,-0.7838],[0.,-2.6436,0.1939,-3.072,-1.0702],[0.,0.,-0.8138,1.5414,0.6155],[0.,0.,0.,-2.6445,-2.1669],[0.,0.,0.,0.,0.0002]])
The expression X.T.dot(X) computes the dot
product of X with its transpose
X.T.
See Table 4-7 for a list of some of the most commonly used linear algebra functions.
4.6 Pseudorandom Number Generation
The numpy.random module
supplements the built-in Python random with functions for efficiently generating
whole arrays of sample values from many kinds of probability
distributions. For example, you can get a 4 × 4 array of samples from the
standard normal distribution using normal:
In[238]:samples=np.random.normal(size=(4,4))In[239]:samplesOut[239]:array([[0.5732,0.1933,0.4429,1.2796],[0.575,0.4339,-0.7658,-1.237],[-0.5367,1.8545,-0.92,-0.1082],[0.1525,0.9435,-1.0953,-0.144]])
Python’s built-in random module,
by contrast, only samples one value at a time. As you can see from this
benchmark, numpy.random is well over an
order of magnitude faster for generating very large samples:
In[240]:fromrandomimportnormalvariateIn[241]:N=1000000In[242]:%timeitsamples=[normalvariate(0,1)for_inrange(N)]732ms+-21.3msperloop(mean+-std.dev.of7runs,1loopeach)In[243]:%timeitnp.random.normal(size=N)43.7ms+-710usperloop(mean+-std.dev.of7runs,10loopseach)
We say that these are pseudorandom numbers
because they are generated by an algorithm with deterministic behavior
based on the seed of the random number generator. You
can change NumPy’s random number generation seed using
np.random.seed:
In[244]:np.random.seed(1234)
The data generation functions in numpy.random use
a global random seed. To avoid global state, you can use
numpy.random.RandomState to create a random number generator isolated from
others:
In[245]:rng=np.random.RandomState(1234)In[246]:rng.randn(10)Out[246]:array([0.4714,-1.191,1.4327,-0.3127,-0.7206,0.8872,0.8596,-0.6365,0.0157,-2.2427])
See Table 4-8 for a partial list of
functions available in numpy.random.
I’ll give some examples of leveraging these functions’ ability to generate
large arrays of samples all at once in the next section.
4.7 Example: Random Walks
The simulation of random walks provides an illustrative application of utilizing array operations. Let’s first consider a simple random walk starting at 0 with steps of 1 and –1 occurring with equal probability.
Here is a pure Python way to implement a single random walk with
1,000 steps using the built-in random
module:
In[247]:importrandom.....:position=0.....:walk=[position].....:steps=1000.....:foriinrange(steps):.....:step=1ifrandom.randint(0,1)else-1.....:position+=step.....:walk.append(position).....:
See Figure 4-4 for an example plot of the first 100 values on one of these random walks:
In[249]:plt.plot(walk[:100])
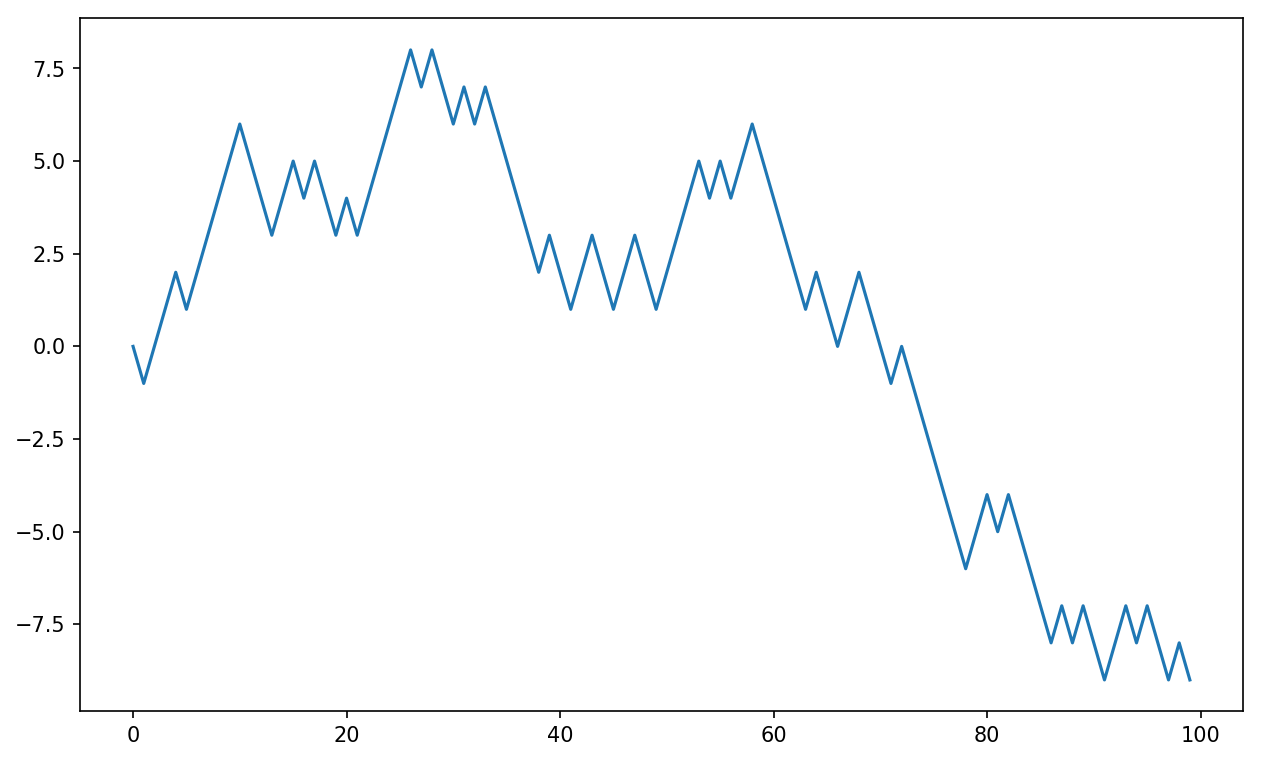
Figure 4-4. A simple random walk
You might make the observation that walk is simply the cumulative sum of the random
steps and could be evaluated as an array expression. Thus, I use the
np.random module to draw 1,000 coin
flips at once, set these to 1 and –1, and compute the cumulative
sum:
In[251]:nsteps=1000In[252]:draws=np.random.randint(0,2,size=nsteps)In[253]:steps=np.where(draws>0,1,-1)In[254]:walk=steps.cumsum()
From this we can begin to extract statistics like the minimum and maximum value along the walk’s trajectory:
In[255]:walk.min()Out[255]:-3In[256]:walk.max()Out[256]:31
A more complicated statistic is the first crossing
time, the step at which the random walk reaches a particular
value. Here we might want to know how long it took the random walk to get
at least 10 steps away from the origin 0 in either direction. np.abs(walk) >=
10 gives us a boolean array indicating where the walk has
reached or exceeded 10, but we want the index of the
first 10 or –10. Turns out, we can compute this
using argmax, which
returns the first index of the maximum value in the boolean array
(True is the maximum value):
In[257]:(np.abs(walk)>=10).argmax()Out[257]:37
Note that using argmax here is
not always efficient because it always makes a full scan of the array. In
this special case, once a True is
observed we know it to be the maximum value.
Simulating Many Random Walks at Once
If your goal was to simulate many random walks, say 5,000 of them,
you can generate all of the random walks with minor modifications to the
preceding code. If passed a 2-tuple, the numpy.random functions will generate a
two-dimensional array of draws, and we can compute the cumulative sum
across the rows to compute all 5,000 random walks in one shot:
In[258]:nwalks=5000In[259]:nsteps=1000In[260]:draws=np.random.randint(0,2,size=(nwalks,nsteps))# 0 or 1In[261]:steps=np.where(draws>0,1,-1)In[262]:walks=steps.cumsum(1)In[263]:walksOut[263]:array([[1,0,1,...,8,7,8],[1,0,-1,...,34,33,32],[1,0,-1,...,4,5,4],...,[1,2,1,...,24,25,26],[1,2,3,...,14,13,14],[-1,-2,-3,...,-24,-23,-22]])
Now, we can compute the maximum and minimum values obtained over all of the walks:
In[264]:walks.max()Out[264]:138In[265]:walks.min()Out[265]:-133
Out of these walks, let’s compute the minimum crossing time to 30
or –30. This is slightly tricky because not all 5,000 of them reach 30.
We can check this using the any method:
In[266]:hits30=(np.abs(walks)>=30).any(1)In[267]:hits30Out[267]:array([False,True,False,...,False,True,False])In[268]:hits30.sum()# Number that hit 30 or -30Out[268]:3410
We can use this boolean array to select out the rows of walks that actually cross the absolute 30
level and call argmax across axis 1
to get the crossing times:
In[269]:crossing_times=(np.abs(walks[hits30])>=30).argmax(1)In[270]:crossing_timesOut[270]:array([735,409,253,...,327,453,447])
Lastly, we compute the average minimum crossing time:
In[271]:crossing_times.mean()Out[271]:498.8897360703812
Feel free to experiment with other distributions for the steps
other than equal-sized coin flips. You need only use a different random
number generation function, like normal to generate normally distributed steps
with some mean and standard deviation:
In[272]:steps=np.random.normal(loc=0,scale=0.25,.....:size=(nwalks,nsteps))
4.8 Conclusion
While much of the rest of the book will focus on building data wrangling skills with pandas, we will continue to work in a similar array-based style. In Appendix A, we will dig deeper into NumPy features to help you further develop your array computing skills.
Get Python for Data Analysis, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

