Chapter 3. Image to Image Mappings
This chapter describes transformations between images and some practical methods for computing them. These transformations are used for warping and image registration. Finally, we look at an example of automatically creating panoramas.
3.1 Homographies
A homography is a 2D projective transformation that maps points in one plane to another. In our case, the planes are images or planar surfaces in 3D. Homographies have many practical uses, such as registering images, rectifying images, texture warping, and creating panoramas. We will make frequent use of them. In essence, a homography H maps 2D points (in homogeneous coordinates) according to
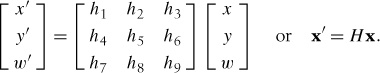
Homogeneous coordinates are a useful representation for points in image planes (and in 3D, as we will see later). Points in homogeneous coordinates are only defined up to scale so that x = [x, y, w] = [αx, αy, αw] = [x/w, y/w, 1] all refer to the same 2D point. As a consequence, the homography H is also only defined up to scale and has eight independent degrees of freedom. Often points are normalized with w = 1to have a unique identification of the image coordinates x, y. The extra coordinate makes it easy to represent transformations with a single matrix.
Create a file homography.py and add the following functions to normalize and convert to homogeneous coordinates:
def normalize(points):
""" Normalize a collection ...Get Programming Computer Vision with Python now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

