ANALYSIS OF MULTIPLE-CHOICE TYPE QUESTIONS
- Question
(L.O. 6) A grandfather wishes to set up a fund today that will allow his grandson to withdraw $5,000 from the fund at the end of each year for four years to pay for college expenses. The first withdrawal is to occur one year from today. How should grandpa compute the required investment if the fund is to earn 6% interest compounded annually and the fund is to be exhausted by the grandson's last withdrawal?
- $5,000 multiplied by the factor for the present value of 1 where n = 4, i = 6%.
- $5,000 divided by the factor for the present value of 1 where n = 4, i = 6%.
- $5,000 multiplied by the factor for the present value of an annuity of 1 where n = 4, i = 6%.
- $5,000 divided by the factor for the present value of 1 where n = 4, i = 6%.
Approach and Explanation: Follow the steps in solving present value problems:
- This is a present value of an annuity problem.
- Time diagram:
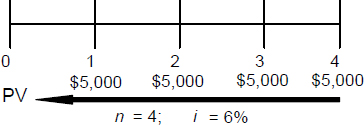
- The factor for present value of an annuity of 1 for n = 4, i = 6% would be derived from Table 4.
- Present Value of an Annuity = Rent × Present Value of an Annuity Factor
Therefore, the present value of the annuity in question equals $5,000 multiplied by the factor for present value of annuity for n = 4, i = 6%. (Solution = c.)
Questions 2 and 3 use the following present value table. Given below are the present value factors for $1.00 discounted at 9% for one to five ...
Get Problem Solving Survival Guide to accompany Financial Accounting, 8th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

