Appendix 3
Stability and Comparison Systems
Study of stability using comparison systems [BOR 74, GRU 76].
A3.1. Vector norms and overvaluing systems
A3.1.1. Definition of a vector norm
Let E = Rn be a vector space and E1, E2,…, Ek be subspaces of E:
![]()
Let x be a vector of Rn for which the projection in subspace Ei is defined by:
[A3.1] ![]()
Note that pi(x) = p(xi) is a scalar norm defined over subspace Ei; it becomes the vector norm:
![]()
If x and y are two vectors of space E and ∀i = 1, 2,..,k, then the following relations are verified:
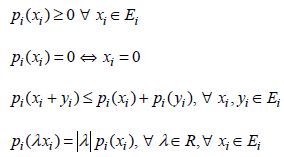
If k−1 subspaces of Ei are insufficient to define the whole of space E, the norm vector is said to be surjective. Furthermore, if every two subspaces Ei are disjoint, the vector norm is said to be regular:
![]()
A3.1.2. Definition of a system overvalued from a continuous process
We define a process for which the evolution into free state is described by the following equation:
The origin is assumed to be the unique equilibrium point of system [A3.1] and this system ...
Get Multiple Models Approach in Automation: Takagi-Sugeno Fuzzy Systems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

