PROBLEMS
6.1. The stability of the feedback control system of Figure P6.1 is to be determined.

Figure P6.1
(a) Determine the system’s P matrix from its state equations.
(b) Find the system’s characteristic equation from knowledge of the P matrix.
(c) Using the Routh–Hurwitz criterion, determine whether this feedback control system is stable.
6.2. Stability of the control system of Figure P6.2 is to be determined.
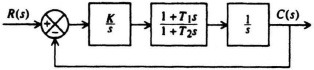
Figure P6.2
(a) Determine the system’s P matrix from its state equations.
(b) Determine the characteristic equation of this system from knowledge of the P matrix.
(c) Utilizing the Routh–Hurwitz criterion, determine the necessary relationship between T1 and T2 for this system to be stable.
6.3. A feedback control system can be represented by a state vector differential equation where
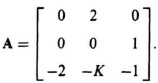
(a) Determine the characteristic equation of this control system.
(b) Using the Routh–Hurwitz criterion, determine the range of K where the system is stable.
6.4. Consider the control system of a tracking radar system which operates in two coordinate axes. Its signal-flow graph, which is illustrated in Figure P6.4 indicates that there is electrical coupling between the control systems ...
Get Modern Control System Theory and Design, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

