2.20. REVIEW OF MATRIX ALGEBRA
The classical methods of describing a linear system by means of transfer functions, block diagrams, and signal-flow graphs have thus far been presented in this chapter. An inherent characteristic of this type of representation is that the system dynamics are described by definable input-output relationships. Disadvantages of these techniques, however, are that the initial conditions have been neglected and intermediate variables lost. The method cannot be used for nonlinear, or time-varying systems. Furthermore, working in the frequency domain is not convenient for applying modern optimal control theory, discussed in Chapter 6 of the accompanying volume, which is based on the time domain. The use of digital computers also serves to focus on time-domain methods. Therefore, a different set of tools for describing the system in the time domain is needed and is provided by state-variable methods. As a necessary preliminary, matrix algebra is reviewed in this section [5, 10].
A matrix A is a collection of elements arranged in a rectangular or square array defined by
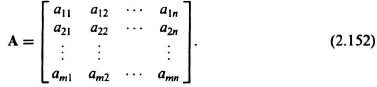
The order of a matrix is defined as the total number of rows and columns of the matrix. For example, a matrix having m rows and n columns is referred to as an m × n matrix. A square matrix is one for which m = n. A column matrix, or vector, is one for which n = 1, and is represented in the ...
Get Modern Control System Theory and Design, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

