Chapter 4
Basic Definitions and Terminology
4.1 Introduction
This chapter is a presentation of basic concepts related to traffic theory, which is a mathematical description of the network and telecommunication systems in probabilistic categories. The aim of traffic theory is to construct analytical models of telecommunication networks and systems that enable their proper design and effective management. Basic principles of traffic theory were formulated by a Danish mathematician Agner Krarup Erlang (1879–1929) at the beginning of the twentieth century. From work originally devoted to telecommunication applications, a new branch of probability theory emerged, called queuing theory. Nowadays, traffic theory is classified as part of technical cybernetics, a branch of science that has been developing very rapidly over the past few decades and has been using an increasing range of mathematical methodologies such as probability theory, algebra, graph theory, stochastic processes theory and Markov process theory.
4.2 Call Stream
The call stream is formed by concatenating calls arriving in random (or otherwise) time moments. Call streams are most commonly described by the following parameters:
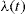 − call intensity − average number of calls (arrivals) during a time interval of length t;
− call intensity − average number of calls (arrivals) during a time interval of length t;- Pk(t) − probability that there are exactly k arrivals during a time interval of length t;
- f(t) − time distribution ...

