The Greek Letters
Let's now take a closer look at this model. First, let us define the cumulative standard normal distribution function because we are going to need this to evaluate Black-Scholes:
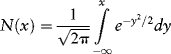
N(x) is bounded between zero and one since it is a probability. Thus, N(d1) for example, substitutes d1 for x in this expression and is increasing in the value of d1 which, itself, is a positive function of the difference between the current spot price S0 and the strike price K as well as the risk-free return but is negatively related to the underlying volatility. From the definitions given earlier, it follows that d2 is also declining in volatility. It is easy to demonstrate using a spreadsheet that both N(d1) and N(d2) are declining in volatility but that their spread is increasing in volatility and this proves that the value of the call option will rise with volatility. The intuition here is that as volatility rises, so does the likelihood that the option will be in the money. This, actually, is the notion of the option's vega—its sensitivity to underlying volatility.
These initial observations give rise to a host of questions regarding the sensitivity of the call option value to changes in the underlying parameters. These questions involve solving for the so-called Greek letters, a topic to which we now turn our attention. I will demonstrate these for the call option. Extension to ...
Get Investment Theory and Risk Management, + Website now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

